Table of contents
1. Introduction
The aim of decision theory is to help decision makers (DM) who face very complex problems choosing between the different possible alternatives, taking into account the consequences of each decision and the DM's preferences (see the definition of the glossary of Cybernetics).
In most practical situations, the difficulty in the act of making a decision results mainly from two problems:
- First, when the DM makes her decision, some data are still uncertain. For
instance, in Lauritzen
and Spiegelhalter (88), a doctor must determine whether her patient
has a dyspnea, a breath illness, so as to give him/her the right
medication. No medical device appropriate to diagnose this illness is
available to the doctor. So her diagnostic can only be based on the
dyspnea's symptoms. Unfortunately, these are quite similar to those of
tuberculosis, lung cancer and bronchitis. A good knowledge of the
patient's activities can help the doctor in her diagnostic. Indeed, journeys
in Asia statistically increase the risk of tuberculosis, smoking is known to
increase lung cancer risks, and so on. The doctor will have certain pieces
of information available, but there will still remain some uncertainty
when she diagnoses the illness.
It may also happen that available data are incomplete. See for instance the ninth chapter of Pearl (88).
- The second problem lies in the number and the complexity of the parameters
(also referred to as attributes or
criteria) that the DM takes into account
to reach her decision. For example, in Keeney and
Raiffa (93), secretary Bracamontes, of the public works ministry, must
advise president Echeverria on the possible construction of a new airport for
Mexico city, and especially on the best location to build it. His advice must
take into account many parameters, including noise pollution, the comfort level
of the neighbor populations, the evolution of air traffic, new runway
construction methods, security, and so on. Here, the complexity results
not only from the high number of criteria, but also from their
interaction. For instance, it is rather clear that the comfort level of the
neighbor populations is intimately related to the level of noise pollution.
Note that the number of criteria to be taken into account can be awfully high. For instance, in Andersen, Andreassen, and Woldbye (86), there are up to 25 relevant criteria which, of course, interact with each other. This gives some insight of how complex practical situations can be.
We can see intuitively that a computer program that can help decision makers making their decisions must rely on two essential components:
- a good modeling of the DM's preferences (in order to make decisions that comply with the DM's desiderata);
- a good management of risks and uncertainties.
Now, what is meant by "a good modeling of the DM's preferences"? When making her decision, the DM has to choose between a certain number of alternatives. Each alternative will have different consequences (also referred to as outcomes). And it is obvious that, for the DM, some consequences will be more appealing than others. The DM can thus "order" the consequences according to their being more or less appealing. Modeling the DM's preferences simply amounts to finding a mathematical or computer model that represents this ordering.
For "small" problems, the ordering may be represented by a two-dimensional array: rows and columns would correspond to the possible consequences, and to each cell of the array would be assigned one of the three following values: "-1" if the outcome corresponding to the row is preferred to that of the column, "0" if the DM is indifferent between the two outcomes, and "1" if the DM prefers the outcome corresponding to the column to that of the row. Once the array is available, extracting the preferences of the decision maker from it is a very easy task. This type of representation, known as pairwise comparison, is quite similar to the arrays of figure 2 in Eckenrode (65).
Of course, when the number of outcomes is high, this modeling is inefficient because the size of the array is way too big. In such cases, other models have to be used, the most popular of which being utility theory.
 |
Table of contents |
2. Utility theory
The principle underlying utility theory is quite simple: it is to assign to each object on which the DM has preferences a real number, in such a way that the higher the number, the preferred the object. Thus, comparing objects amounts to comparing their associated numbers, which is a trivial task for a computer. The DM expresses her preferences through a set of attributes (or criteria). Each attribute can take a certain number of values (aka levels of satisfaction). For instance, when you wish to buy a car, your comparison of the different cars available on the market will certainly be based on their brand, their price, their color, their level of comfort, and so on. So each car can be represented as a tuple (price,brand,etc). The objects can thus be represented as tuples of levels of satisfaction of attributes, and modeling the DM's preferences over these objects thus amounts to evaluate a multiple argument real valued function. This is precisely what we call a utility function. In mathematical terms:
Let \(X\) be the set of objects over which the DM has preferences and \(\mathbb{R}\) be the set of real numbers. Let \(\succsim\) be the DM's preference relation, that is, \(x \succsim y\) means that the DM prefers \(x\) to \(y\) or is indifferent between \(x\) and \(y\).
\(f : X \mapsto \mathbb{R}\) is a utility function representing \(\succsim\) if and only if: \[x \succsim y \Longleftrightarrow f(x) \geq f(y)\ \forall\ x,y \in X.\]
When there are multiple attributes, the sets of levels of satisfaction of which are the \(X_i\)'s, \(i \in \{1,\ldots,n\}\), the object set \(X\) can be represented as \(X = X_1 \times X_2 \times \cdots \times X_n\). A function \(f : X \mapsto \mathbb{R}\) is then a utility function representing \(\succsim\) if and only if: \[(x_1,\ldots,x_n) \succsim (y_1,\ldots,y_n) \Longleftrightarrow f(x_1,\ldots,x_n) \geq (y_1,\ldots,y_n)\ \forall (x_1,\ldots,x_n),(y_1,\ldots,y_n) \in X.\]
Utility functions are computationally very attractive because they provide easy and fast ways to extract the DM's preferences. Moreover, unlike the pairwise comparison method, in many practical situations, they do not usually consume huge amounts of memory.
 |
Table of contents |
3. Decision under certainty, risk or uncertainty
As we saw in section 2.1, the DM's preferences over the set of possible alternatives are related to the consequences induced by these alternatives. As an illustration, Savage (54) gives the following example: your wife is cooking an omelet. She has already broken five eggs in a plate and she asks you to complete the cooking. There remains one unbroken egg and you wonder whether you should put it in the omelet or not. Here, you have three possible alternatives:
- you can break the egg in the plate containing the other eggs;
- you can break it into another plate and examine it before mixing it with the five other eggs;
- you can not use the egg.
How can we find the best suitable decision? Well, simply by examining the consequences of each decision. Thus, if the egg is good the first alternative should be better than the other ones because the omelet will be bigger, but if it is not, by choosing the first alternative, we loose the five other eggs. If we choose the second alternative and the egg is good, we stain a dish that we will have to wash, and so on. By closely examining the consequences of each alternative, we should be able to select the one that seems to be the most preferable.
As shown in this example, each alternative may have several consequences depending on whether the egg is good or not. In Decision Theory, these uncertain factors (here the state of the egg) are called events and, as in Probability Theory, elementary (or atomic) events are very important. They are called states of nature. To each state of nature (the egg is good or not), the choice of one of the three possible alternatives will induce a unique consequence. Thus alternatives can be represented as sets of pairs (event, consequence), which are called acts. More formally, let \({\cal A}\) be the set of possible alternatives, \(X\) be the set of all possible consequences, and \({\cal E}\) the set of states of nature. An act is a mapping from \({\cal E}\) to \(X\) that assigns to each state \(e \in {\cal E}\) a consequence in \(X\). Thus the constant act \(f\) corresponding to choosing the first alternative (break the egg in the plate containing the other eggs) is such that \(f\)(good egg) = "big omelet" and \(f\)(bad egg) = "lose 5 eggs".
As alternatives can be represented by acts, we can associate to the DM's preference relation over alternatives a preference relation over the set of acts (see Savage (54) or von Neumann & Morgenstern (44) for a detailed discussion on this matter). Let us denote by \(\succsim_{\cal A}\) this preference relation. A utility function representing \(\succsim_{\cal A}\) is thus a mapping \(U\) from \({\cal A}\) to \(\mathbb{R}\) such that: \[\mbox{act}_1 \succsim_{\cal A} \mbox{act}_2 \Longleftrightarrow U(\mbox{act}_1) \geq U(\mbox{act}_2).\]
Of course, preferences over acts reveal both preferences over consequences (the DM will certainly prefer having a big omelet than losing five eggs) and the DM's belief in the chances that each event obtains. Thus if the DM knows that his wife is very careful about the food she keeps in her fridge, the impact of the pair (bad egg, lose 5 eggs) in the evaluation of alternative 1 will be marginal, whereas it will become important if the DM knows that his wife usually does not pay attention to this sort of things. Thus function \(U\) must take into account the plausibility of realisation of the events. Of course, this can be done only through the knowledge that the DM has of the events and not through their "true" plausibility of realisation because the decisions chosen by the DM are only based on what he/she knows. For instance, consider a decision inducing two different consequences depending on whether head or tail obtains when tossing a fair coin. You do not know that the coin is fair, but I tossed the coin thrice and you saw that two heads and one tail obtained. So your decision will be based on the fact that the chance of obtaining a head seems higher than that of having a tail, although in practice they have the same chance of realisation. Of course, different kinds of knowledge will involve different models for function \(U\). The following three are the most important ones in Decision Theory:
- Decision under certainty: for every state
of nature, a given act has always the same consequence. For instance, when you
decide to choose a menu rather than another one in a restaurant, consequences
are known for sure: you know what you will eat (well, at least this should be).
Let \(\succsim_{\cal A}\) be the preference relations over the set of acts and \(\succsim\) be that over the set of consequences. Assume that \(\succsim_{\cal A}\) and \(\succsim\) are represented by \(U: {\cal A} \mapsto \mathbb{R}\) and \(f : X \mapsto \mathbb{R}\) respectively. Let \(x_{\mbox{act}}\) denote the consequence of "act". Then Decision under certainty amounts to: \[\mbox{for all act} \in {\cal A},\ U(\mbox{act}) = f(x_{\mbox{act}}).\]
- Decision under risk: An act can have
several consequences, depending on the realisation of some event. Moreover, an
"objective" probability distribution over the events is supposed to exist and
to be known by the DM. This is the case when you decide whether to gamble or not
on a game such as loto: the probability of winning is known. The model used in
decision under risk is called the expected utility
model and has been axiomatised by
von Neumann & Morgenstern (44). As an act can be
represented by pairs (event,consequence) and as there exist probabilities on events, acts can be
represented by sets of pairs (consequence, probability of the consequence).
These sets are usually called lotteries. Thus
assume that an act corresponds to the lottery \(\langle x^1,p_1;\ldots;x^n,p_n \rangle\),
i.e., this act has consequence \(x^1\) with probability \(p_1\), \(x^2\) with probability
\(p_2\) and so on. Then von Neumann-Morgenstern show that function \(U\) representing
preferences over acts is decomposable as:
\[U(\mbox{act}) = \sum_{i=1}^n p_i f(x^i).\]
where \(f : X \mapsto \mathbb{R}\) is a utility function representing the DM's preferences over the outcomes.
- Decision under uncertainty: this is
quite similar to the preceding case except that we do not assume the
existence of a probability distribution on the events set but rather this
one is derived from a set of axioms (see Savage (54))
that express that fact that the DM has a "rational" behaviour. Here the probability
distribution is not "objective" as in von Neumann-Morgenstern's theory but
it is subjective, that is, it expresses the beliefs of the DM concerning the
chances of realisation of the events (instead of the "true" chance that the
event will obtain). In this model, as in von Neumann-Morgenstern, the utility
\(U\) of an act is decomposable as:
\[U(\mbox{act}) = \sum_{i=1}^n p_i f(x^i).\]
where \(f : X \mapsto \mathbb{R}\) is a utility function representing the DM's preferences over the outcomes, and \(p_i\) is the subjective probability that the DM assigns to the event that resulted in \(x^i\).
In the remaining of this tutorial, we will study only decision under certainty.
 |
Table of contents |
4. Additive utility theory under certainty
When I said that utility functions do not consume huge amounts of memory, well, shame on me, I lied. In fact, in the general case, they require as much memory as pairwise comparison tables and, moreover, their construction is a nightmare as they require asking many cognitively difficult questions to the DM. Fortunately, in most practical situations, a property called additive separability holds, that enables tremendous memory savings and that requires to ask the DM only "simple" questions to construct the whole utility function. We saw that the outcome set \(X\) can be an \(n\)-dimensional set \(X = X_1 \times X_2 \times \cdots \times X_n\) and thus utility functions are multiple parameters functions. Suppose that there are 5 attributes and that each one has 10 levels of satisfactions, then the outcome set \(X\) is a \(5^{10}\) = 9765625 element set and, to store the utility function into memory, up to 9765625 bytes (or words) may be needed. If, on the other hand, the utility function can be separated as follows: \[f(x_1,\ldots,x_n) = f(x_1) + \cdots + f_n(x_n),\] then storing each \(f_i(x_i)\) requires only 10 bytes, and the whole utility is stored in at most 50 bytes, which seems to be a reasonable amount for modern computers. Such a utility function is called an additive utility function. In mathematical terms:
Additive utilities are computationally much more appealing than general utility functions. We have seen that they reduce tremendously the memory storage requirements, but this is not the only advantage: Let us recall that these functions are used to represent the DM's preference relations. When the utility is additively separable, this means that there exists some kind of independence between the attributes, and this independence makes the elicitation of the utility much easier to perform. The following example may help understanding why:
Let \(\succsim\) be a preference relation over a set \(X = X_1 \times X_2\). Suppose that \(\succsim\) is representable by an additive utility function \(f_1(x_1) + f_2(x_2)\) and that \((x_1,x_2) \succsim (y_1,x_2)\). By definition 2, the following equation holds: \[f_1(x_1) + f_2(x_2) \geq f_1(y_1) + f_2(x_2)\] which is obviously equivalent to \(f_1(x_1) \geq f_1(y_1)\). But then, for all \(y_2 \in X_2\), we have that: \[f_1(x_1) + f_2(y_2) \geq f_1(y_1) + f_2(y_2).\] Thus, again by definition 2, \((x_1,y_2) \succsim (y_1,y_2)\). In other words, the existence of an additive utility allowed us to prove that \((x_1,y_2) \succsim (y_1,y_2)\) does not depend on the value of \(y_2\). This simple remark simplifies considerably the utility elicitation procedure.
Another advantage of additive utility functions lies in their computation: thanks to the additive separability, they are usually very simple mathematical functions and therefore they can be usually computed very quickly, especially when using parallel algorithms.
Unfortunately, not all utility functions are additively separable, as shown in the following example, taken from Fishburn (70), page 42:
Suppose that you have to choose between chicken and fish for today's and tomorrow's dinners. Then \(X = \{\mbox{chicken today}, \mbox{fish today}\} \times \{\mbox{chicken tomorrow}, \mbox{fish tomorrow}\}\). If you always have to choose between these two meals, one day you will get bored of eating the same meal, and you will have a preference relation much like the following: \[\begin{eqnarray*} & (\mbox{fish today}, \mbox{chicken tomorrow}) \succ (\mbox{chicken today}, \mbox{fish tomorrow}) & \\ & \quad\quad\quad\quad\succ (\mbox{fish today}, \mbox{fish tomorrow}) \succ (\mbox{chicken today},\mbox{chicken tomorrow}). & \end{eqnarray*}\] In such a case, the attributes are not independent. Indeed, what you prefer eating tomorrow is conditioned by what you eat today. One consequence is that the utility elicitation process requires a huge number of comparisons between elements of \(X\).
 |
Table of contents |
5. Existence of additive utilities
As is shown in the above example, all utilities are not additively separable. So, it would be very interesting to know in which cases preference relations can be represented by additive utility functions and in which ones they cannot.
From a theoretical point of view, necessary and sufficient conditions have been provided that ensure additive representability; see for example Jaffray (74b) for conditions in two-dimensional outcome sets, Jaffray (74a) for conditions on sets of arbitrary finite dimensions, Fishburn (92) for an extension of these results. In their ninth chapter, Krantz, Luce, Suppes and Tversky, A. (1971) also provide interesting necessary and sufficient conditions. However, from a practical point of view, the results mentioned above are very difficult to use because they are highly technical. The alternative, often used in additive conjoint measurement (this is the true name for the theory of additive utilities), is to provide only sufficient -- but easily testable -- conditions of existence.
In most research papers, for mathematical reasons, it is assumed that the set of outcomes \(X\) is a Cartesian product (of levels of satisfaction of attributes). Note that there exist a few papers that provide testable (sufficient) conditions for the case where \(X\) is a subset of a Cartesian product. Let us cite for instance Chateauneuf and Wakker (93), Segal (91) and Segal (94).
In the sequel, we will assume that \(X\) is an \(n\)-dimensional Cartesian product, i.e., that: \[X = \prod_{i=1}^n X_i.\] Given a binary relation \(\succsim\) over \(X\), I introduce the indifference relation \(x \sim y \Longleftrightarrow [x \succsim y\) and \(y \succsim x]\), i.e., this is the symmetric part of \(\succsim\), the strict preference relation \(x \succ y \Longleftrightarrow [x \succsim y\) and Not\((y \succsim x)]\), and \(x \precsim y \Longleftrightarrow y \succsim x\). Now, let us see some necessary conditions for the existence of additive utilities representing \(\succsim\).
 |
Table of contents |
5.1. Necessary conditions
Suppose that an additive utility \(f : X \mapsto \mathbb{R}\) exists, representing \(\succsim\), i.e., for all \(x=(x_1,\ldots,x_n)\) and all \(y = (y_1,\ldots,y_n)\), \[f(x) = \sum_{i=1}^n f(x_i), \quad f(y) = \sum_{i=1}^n f(y_i) \quad \text{and} \quad x \succsim y \Longleftrightarrow f(x) \geq f(y). \] Then, clearly, the following axiom holds:
- \(\succsim\) is complete: for all \(x,y \in X\), \(x \succsim y\) or \(y \succsim x\),
- \(\succsim\) is transitive: for all \(x,y,z \in X\), \(x \succsim y\) and \(y \succsim z \Longrightarrow x \succsim z.\)
Now, suppose that \((x_1\ldots,x_{i-1},x_i,x_{i+1},\ldots,x_n) \succsim (y_1\ldots,y_{i-1},x_i,y_{i+1},\ldots,y_n)\) and that \(\succsim\) is representable by an additive utility \(f\). Then, we have that: \[f_i(x_i) + \sum_{j \neq i} f_j(x_j) \geq f_i(x_i) + \sum_{j \neq i} f_j(y_j).\] But this inequality is obviously equivalent to: \[f_i(y_i) + \sum_{j \neq i} f_j(x_j) \geq f_i(y_i) + \sum_{j \neq i} f_j(y_j)\] for all \(y_i \in X_i\), which, in turn, is equivalent to: \[(x_1\ldots,x_{i-1},y_i,x_{i+1},\ldots,x_n) \succsim (y_1\ldots,y_{i-1},y_i,y_{i+1},\ldots,y_n).\] Therefore, the following axiom, which is sometimes referred to as coordinate independence (see e.g. Wakker (89), page 30), is necessary for additive representability.
Note that the independence axiom enables to define, for every subset \(N \subseteq \{1,\ldots,n\}\), the weak order \(\succsim_N\) on \(\prod_{i \in N} X_i\) as: for all \(a,b \in \prod_{i \in N} X_i\), \(a \succsim_N b\) if and only if \((a,p) \succsim (b,p)\) for some \(p \in \prod_{i \not\in N} X_i\). In particular, \(\succsim_{12}\) is the weak order induced by \(\succsim\) on \(X_1 \times X_2\), i.e., for all \(x,y \in X_1 \times X_2\), \(x \succsim_{12} y \Longleftrightarrow [\) there exists \(p \in \prod_{i \geq 3} X_i\) such that \((x,p) \succsim (y,p)]\).
Using an argument similar to that used for showing that Axiom 2 is necessary for additive representability, it is easily shown that the axiom below, namely the Thomsen condition, is necessary as well.
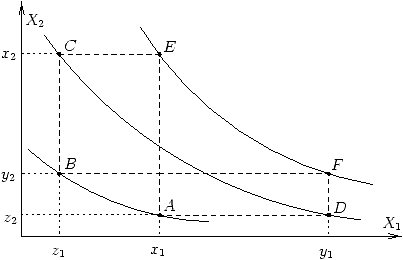
The above figure illustrates the Thomsen condition. The curves passing through points A and B, C and D, and E and F are called indifference curves. They represent points in the outcome set that are considered all indifferent (from the Decision Maker's point of view). The first indifference in the Thomsen condition is simply illustrated by the fact that A and B belong to the same indifference curve. Similarly, the second indifference means that C and D belong to the same indifference curve. Then the Thomsen condition implies that E and F must also belong to the same indifference curve. Note that by permuting the order of variables \(x_1,x_2,y_1,y_2,z_1,z_2\), the Thomsen condition would also imply that if A and B, and E and F belong to the same indifference curves, then this is also the case for C and D.
Unfortunately, even though the above axioms are necessary, they are not sufficient to ensure additive representability. For instance, if \(\succsim\) on \(X = \{0,1,2,3\}^2\) is represented by \(f\), as defined in table 1,
| \(x_1\) \ \(x_2\) | 0 | 1 | 2 | 3 |
| 0 | 0 | 3 | 6 | 9 |
| 1 | 6 | 9 | 12 | 18 |
| 2 | 15 | 21 | 24 | 27 |
| 3 | 24 | 30 | 33 | 36 |
then \(\succsim\) satisfies weak ordering; independence holds because \(f(x_1,x_2)\) increases with \(x_1\) and \(x_2\); there exist neither distinct \(x_1,y_1,z_1 \in X_1\) nor distinct \(x_2,y_2,z_2 \in X_2\) such that \((x_1,z_2) \sim (z_1,y_2)\) and \((z_1,x_2) \sim (y_1,z_2)\), so that the Thomsen condition trivially holds on \(X\). However, no additive utility \(v\) represents \(\succsim\) else: \[\begin{eqnarray*} v_1(0) + v_2(3) & = & v_1(1) + v_2(1), \\ v_1(1) + v_2(0) & = & v_1(0) + v_2(2) \mbox{ and} \\ v_1(2) + v_2(2) & = & v_1(3) + v_2(0) \mbox{ would imply that}\\ v_1(3) + v_2(1) & = & v_1(2) + v_2(3). \end{eqnarray*}\] And this is impossible since \(v(3,1) = 30 > 27 = v(2,3)\).
More generally, using arguments similar to that used for independence, it is rather straightforward to show that additive representability requires, for all \(m \in \mathbb{N}\), the following axiom.
Note that independence and the Thomsen condition are special cases of cancellation axioms. Note also that if the (\(m+1\))st-order cancellation axiom holds, the \(m\)th-order one clearly also holds. From a theoretical point of view, cancellation axioms are useful since they are necessary conditions for additive representability (when the sets \(X_i\)'s are finite, the infinite-order cancellation axiom is even sufficient to ensure additive representability: see Adams (65)). But they are difficult to handle in practical situations when their order increases because they require to test numerous preference relations. Therefore, only those of low order can be easily tested. To circumvent this difficulty, in the finite case, i.e., when the \(X_i\)'s are finite, Scott (64) showed that additive representability amounted to solving a system of linear inequalities. In the infinite case --- the case studied in this web page --- one way out is to assume some (nonnecessary) structural conditions which enable to derive any cancellation axiom from independence and the Thomsen condition. Such structural conditions are connectedness of topological spaces (see Debreu (60) and Wakker (89)), or solvability w.r.t. every component (Krantz, Luce, Suppes and Tversky (71)).
 |
Table of contents |
5.2. Structural conditions
In the rest of this page, I will only speak of a particular form of solvability called restricted solvability. If you are interested in the connectedness conditions, read the excellent book Wakker (89). In the beginning of the sixties, some researchers gave structural conditions they called "solution of equations" (Luce Tukey (64)), "solvability" (Krantz (64)) and "unrestricted solvability" (Fishburn (70)). These were the first form of structural conditions used to ensure the existence of additive utility functions. Later, researchers provided a more general condition called restricted solvability. This condition is still used nowadays.
In many problems in economics, the \(X_i\)'s can be thought of as continuous: consider for instance attributes like money, time, infinitely divisible consumer goods, etc. In such cases, the above axiom can be assumed safely.
Usually, the structure induced by restricted solvability is strong enough to ensure that some high-order cancellation axioms can be derived from some low-order ones. This is particularly useful for the elicitation of additive utility functions since only independence and the Thomsen condition need be checked. However, restricted solvability alone is not strong enough to ensure additive representability, as is shown in the following example:
Let \(X = X_1 \times \mathbb{N}\), where \(X_1 = \mathbb{R} \times \mathbb{R}\). Let \(\succsim\) be a preference relation on \(X\) such that:
- for all \(x_1\) in \(X_1\) and for all \(x_2,y_2 \in \mathbb{N}\), \((x_1,x_2) \sim (x_1,y_2)\),
- for all \(x_1,y_1 \in X_1\) and for all \(x_2 \in \mathbb{N}\), \((x_1,x_2) \succsim (y_1,x_2) \Longleftrightarrow x > y\) or \((x = y\) and \(x' \geq y')\), where \(x_1=(x,x')\), \(y_1=(y,y')\) and \(x,x',y,y' \in \mathbb{R}\).
It can be easily shown that restricted solvability holds w.r.t. both \(X_1\) and \(\mathbb{N}\):
- if \((y_1^0,y_2) \precsim (x_1,x_2) \precsim (y_1^1,y_2)\), then, by Property 1, \((x_1,x_2) \sim (x_1,y_2)\);
- if \((y_1,y_2^0) \precsim (x_1,x_2) \precsim (y_1,y_2^1)\), then, by Property 2, \((y_1,y_2^0) \precsim (x_1,x_2)\) implies that \(x > y\) or \((x = y\) and \(x' \geq y')\), and \((x_1,x_2) \precsim (y_1,y_2^1)\) implies that \(x < y\) or \((x = y\) and \(x' \leq y')\), so that, necessarily, \(x_1 = y_1\). Hence, by Property 1, for all \(y_2\), \((x_1,x_2) \sim (y_1,y_2)\).
Similarly, independence trivially holds. As for the Thomsen condition, if \((x_1,z_2) \sim (z_1,y_2)\) and if \((z_1,x_2) \sim (y_1,z_2)\), then \(x_1 = y_1 = z_1\). Hence, \((x_1,x_2) \sim (y_1,y_2)\). However \(\succsim\) is not representable by an additive utility function. Indeed, if it were, the lexicographic ordering on \(X_1 = \mathbb{R} \times \mathbb{R}\) would also be additively representable, which is known to be impossible.
In this example, two problems prevent additive representability. The first one, the easiest to fix, is simply that the second attribute of \(X\) is useless since for all \(x_1,x_2,y_2\), \((x_1,x_2) \sim (x_1,y_2)\). Hence, even if it satisfies restricted solvability, it cannot structure the outcome space. In such a case, we say that this attribute is inessential. To prevent this, the following axiom shall be used:
The second problem highlighted in Example 3 is that it may happen that the outcome space has so many elements that it cannot be represented by real valued functions. This is precisely the case of the lexicographic order on \(\mathbb{R} \times \mathbb{R}\). Therefore, to ensure additive representability, we need another axiom that guarantees that the outcome space has no more elements than the set of the real numbers. This axiom is usually an Archimedean axiom. Note that the latter needs not always be explicitly stated: condition (H) in Jaffray (74b) is a necessary and sufficient condition for additive representability, closely related to cancellation axioms and which includes implicitly an Archimedean property; similarly, connectedness and separability of the topological spaces in the topological approach to additive conjoint measurement ensure the Archimedean property. However, in this web page, it must be explicitly stated. The Archimedean axiom as stated in the classical theorems is illustrated in figure 1.
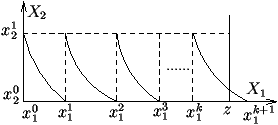
For simplicity, assume that \(X = \mathbb{R} \times \mathbb{R}\) and that \(\succsim\) is representable by an additive utility function \(f\). Let \(x_1^0\), \(x_2^0\) and \(x_2^1\) be arbitrary elements of \(\mathbb{R}\) such that \(x_2^1 \succ_2 x_2^0\). Then \(a = f_2(x_2^1) - f_2(x_2^0) > 0\). Let \(x_1^1\) be such that \((x_1^1,x_2^0) \sim (x_1^0,x_2^1)\). Then, by definition of Function \(f\), \(f_1(x_1^1) + f_2(x_2^0) = f_1(x_1^0) + f_2(x_2^1)\), or, equivalently, \(f_1(x_1^1) = f_1(x_1^0) + a\). Similarly, let \(x_1^2\) be such that \((x_1^2,x_2^0) \sim (x_1^1,x_2^1)\). Then \(f_1(x_1^2) = f_1(x_1^1) + a\), or equivalently, \(f_1(x_1^2) = f_1(x_1^0) + 2a\). By induction, it is obvious that, at the \(k\)th step, one gets \(f_1(x_1^k) = f_1(x_1^0) + ka\). So, when \(k\) tends toward infinity, \(f_1(x_1^k)\) also tends toward infinity. If there exists an element \(z \in X\) such that \(z \succ (x_1^i,x_2^0)\) for all \(i\)'s in a sequence, then, since \(f\) is a utility function, \(f(z)\) has a finite value such that \(f(z) > f_1(x_1^i) + f_2(x_2^0)\). Therefore, Sequence \((x_1^i)\) --- which is usually referred to as a standard sequence --- must be finite. Of course, a similar result should hold when the sequence is constructed from right to left, instead of from left to right as in figure 1. This suggests the following definition and axiom.
- Not\([(x_1^0,x_2^0,\ldots,x_n^0) \sim (x_1^0,x_2^1,\ldots,x_n^1)]\),
- \((x_1^{k+1},x_2^0,\ldots,x_n^0) \sim (x_1^k,x_2^1,\ldots,x_n^1)\) for all \(k,k+1 \in N\).
 |
Table of contents |
5.3. Existence theorems
In the late sixties/beginning of the seventies, researchers proved, using semigroups (see Krantz, Luce, Suppes and Tversky, A. (1971)), that the above axioms were sufficient for additive representability. Two representation theorems were given, depending on the number of dimensions of Cartesian product \(X\):
Note the uniqueness properties in both theorems: when restricted solvability holds, additive utilities are unique up to scale (the \(a\) constant) and location (the \(b_i\)'s). Remind that restricted solvability is a structural condition and therefore is not necessary for additive representability. When it does not hold, but additive utilities do exist, those are generally not unique up to scale and location, as is shown in the example below. This shows how strong an assumption is restricted solvability.
 |
Table of contents |
6. References
- Adams, E. W. (1965) "Elements of a Theory of Inexact Measurement", Philosophy of Science, Vol. 32, pp. 205--228.
- Andersen, S K, Andreassen, S and Woldbye, M (1986) "Knowledge Representation For Diagnosis And Test Planning in The Domain of Electromyography", in Proceedings of the 7th European Conference on Artificial Intelligence, pp. 357--368, Brighton.
- Chateauneuf, A. and Wakker, P. P. (1993) "From Local to Global Additive Representation", Journal of Mathematical Economics, Vol. 22, pp. 523--545.
- Debreu, G. (1960) "Topological Methods in Cardinal Utility Theory", in Mathematical Methods in the Social Sciences, ed. by K. J. Arrow, S. Karlin and P. Suppes, pp. 16--26. Stanford University Press, Stanford, CA.
- DeFinetti, Bruno. "Theory of Probability", Vol 1 & 2, Wiley & Sons.
- Eckenrode, R. T. (1965) "Weighting Multiple Criteria", Management Science, Vol 12(3), pp. 180--192.
- Fishburn, P. C. (1970) "Utility Theory for Decision Making". Wiley, NewYork.
- Fishburn, P. C. (1992) "A General Axiomatization of Additive Measurement with Applications", Naval Research Logistics, Vol 39, pp. 741-755.
- Jaffray, J.-Y. (1974a) "Existence, Propriétés de Continuité, Additivité de Fonctions d'Utilité sur un Espace Partiellement ou Totalement Ordonné", Thèse d'État, Université Paris VI.
- Jaffray, J.-Y. (1974b) "On the Extension of Additive Utilities to Infinite Sets", Journal of Mathematical Psychology, Vol 11(4), pp. 431--452.
- Keeney, R. L. and Raiffa, H (1993) "Decisions with Multiple Objectives - Preferences and Value Tradeoffs". Cambridge university Press.
- Krantz, D. H. (1964) "Conjoint Measurement: The Luce-Tukey Axiomatization and Some Extensions", Journal of Mathematical Psychology, Vol. 1, pp. 248--277.
- Krantz, D. H., Luce, R. D., Suppes, P., and Tversky, A. (1971) "Foundations of Measurement(Additive and Polynomial Representations)", Vol. 1. Academic Press, New York.
- Lauritzen, S. L., and Spiegelhalter, D. J.(1988) "Local Computations with Probabilities on Graphical Structures and Their Application to Expert Systems", The Journal of The Royal Statistical Society - Series B (Methodological), Vol 50(2), pp. 157--224.
- Lindley, Dennis V (1982). "Scoring Rules and the Inevitability of Probability", International Statistical Review, Vol 50, pp. 1-26.
- Luce, R. D. and Tukey, J. W. (1964) "Simultaneous Conjoint Measurement: A New Type of Fondamental Measurement", Journal of Mathematical Psychology, Vol. 1, pp. 1--27.
- Pearl, J (1988). "Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference". Morgan Kaufman Publishers, inc, San Mateo, California.
- Principia Cybernetica. "Glossary of Cybernetics", http://pespmc1.vub.ac.be/ASC/INDEXASC.html.
- Savage, L.J. (1954). "The Foundations of Statistics". Dover.
- Scott, D. (1964). "Measurement structures and Linear Inequalities", Journal of Mathematical Psychology, Vol. 1, pp. 233--247.
- Segal, U. (1991). "Additively Separable Representations on Non-convex Sets", Journal of Economic Theory, Vol. 56, pp. 89--99.
- Segal, U. (1994). "A Sufficient Condition for Additively Separable Functions", Journal of Mathematical Economics, Vol. 23, pp. 295--303.
- von Neumann, J. and Morgenstern, O. (1944). "Theory of Games and Economic Behaviour". Princetown University Press, Princetown, New Jersey.
- Wakker, P. P. (1989). "Additive Representations of Preferences, A New Foundation of Decision Analysis", Kluwer Academic Publishers, Dordrecht.
 |
Table of contents |
