RandCubComplex: generation of 3D cubical complexes
RandCubComplex is a simple program for generating random 3D cubical complexes. It is created for testing our software ViteBetti.
The main function of this program is to generate random cubical complex. This can be done in two ways: (1) by adding cubes—and their faces—to an empty cubical complex or (2) by removing cubes—and their cofaces— from the full cubical complex. Other parameters are the size along each axis, the probability of adding/removing a cube and the range of dimensions of the cubes that are added/removed.
We can try more complex constructions by combining several cubical complexes. RandCubComplex allows us to make the union (A∪B), the intersection (A∩B) and the difference (A∖B) of two cubical complexes.
Data format
The cubical cells of a 3D cubical complex are of the form [x, x+d1]×[y, y+d2]×[z, z+d3] where di is 1 or 0. Thus, a cubical cell can be unequivocally identified to a vector (2x+d1, 2y+d2, 2z+d3). Therefore, a 3D cubical complex can be easily encoded as a binary three-dimensional array A where the position A(i,j,k) is 1 if the corresponding cubical cell belongs to the complex or 0 otherwise.
A text file describing a 3D cubical complex consists in:
- A first line with the size of the bounding box along each axis;
- The content of the tree-dimensional array A running first in the z-coordinate, next in the y-coordinate and last in the x-coordinate.
You can see here a small 3D cubical complex with Betti numbers (1,1,1).
Download and compile
You can download the source code here. After extracting the source files you can compile them on Linux as follows:
g++ main.cpp cubcomplex.cpp -O3 -o RandComplex
Usage
You have four options in RandCubComplex for generating 3D cubical complexes.
- Make
-
This generates a random 3D cubical complex by adding or removing cubes with a given probability. This function requires 7 arguments. You can use it by writing:
./RandCubComplex -m size_x size_y size_z probability make_mode min_dim max_dim -o output_file
where- -m or --make establishes the make mode.
- size_x, size_y, size_z are the sizes of the cubical complex along the three axes. Note that these three values must be odd integers.
- Each cube is affected with uniform probability p=probability, though this can affect its faces or cofaces.
- make_mode=1 adds cubes to the empty cubical complex, while make_mode=0 removes cubes from the full cubical complex.
- [min_dim, max_dim] is the range of cubes that are added/removed.
- output_file is the name of the file containing the resulting 3D cubical complex. This is output.dat by default.
./RandCubComplex -m 101 51 51 0.35 1 1 2 -o complex1.datcreates an empty cubical complex of size 101x51x51 and add each 1- or 2-cube with uniform probability p=0.35. The resulting cubical complex is saved as complex1.dat. Note that this complex also contains 0-cubes, namely the 0-dimensional faces of the 1- and 2-cubes added. Also, there may be 1-cubes that were added because they were faces of an added 2-cube.
On the other hand,./RandCubComplex -m 101 51 51 0.35 0 1 1 -o complex2.datcreates a full cubical complex and removes the 1-cubes with uniform probability p=0.35. Consequently, some 2- and 3-cubes are also removed (their cofaces). - Union
- This option takes two complexes (with the same sizes) and returns their union. Usage:
./RandCubComplex -u complex1.dat complex2.dat -o complex3.dat. - Intersection
- This option takes two complexes (with the same sizes) and returns their intersection. Usage:
./RandCubComplex -i complex1.dat complex2.dat -o complex3.dat. - Difference
- This option takes two complexes (with the same sizes) and returns their difference. Usage:
./RandCubComplex -d complex1.dat complex2.dat -o complex3.dat.
Two examples
It seems that the Betti numbers of a complex where only 3-cubes are added (./RandCubComplex -m 101 101 101 0.3 1 3 3) are related to the Betti numbers of a complex where only 0-cubes are removed (./RandCubComplex -m 101 101 101 0.3 0 0 0) coincide. After creating several many complexes of both types using different proportions, we obtain the following graphics:

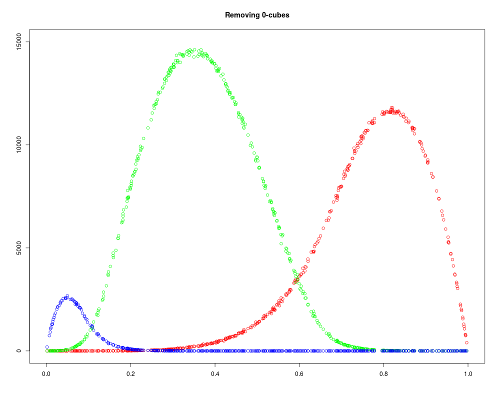
We can observe that they are very similar (after reversing the dimension of the Betti numbers) and we can expect that they converge to the same graphic as the size tends to infinity.
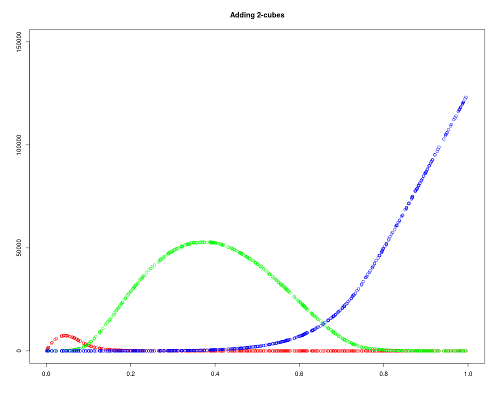
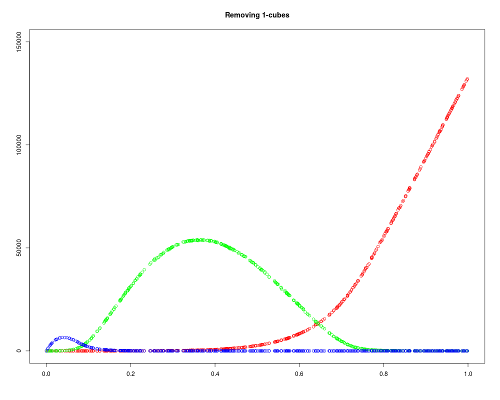
We can also ask ourselves what happens when we add 2-cubes (./RandCubComplex -m 101 101 101 0.3 1 2 2) and when we remove 1-cubes (./RandCubComplex -m 101 101 101 0.3 0 1 1). Once again, we obtain similar graphics: