Thickness and Breadth
You can find here some examples of the breadth and the thickness of the homology groups of binary volumes.
These meshes are available in AIM@SHAPE. They were voxelized with binvox. The signed distance transform is computed with DGtal and the persistent intervals, with a specific software. The output is rendered with Blender. Also, the diagrams are made with RStudio.
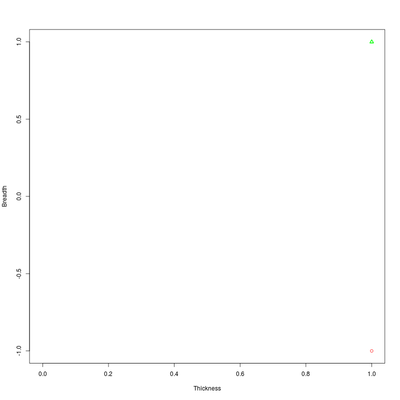
Each binary volume is accompanied by its thickness-breadth diagram. Every 0-hole (connected component), 1-hole (handle, tunnel) or 2-hole (void, cavity) is associated to a thickness-breadth pair (x,y). These pairs are represented as points in the thickness-breadth diagram. Concretely, 0-holes are despicted as red circles, 1-holes as green triangles and 2-holes as blue squares.
Next, we represent all or some of these measures as 3D balls on the complex. Thickness values are shown as balls contained in the volume, while breadth values are outside. We usually only show the balls associated to the 1-holes.
Fertility

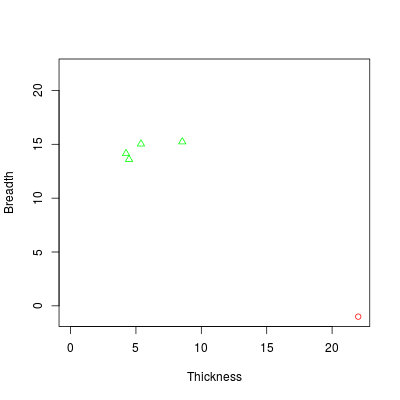
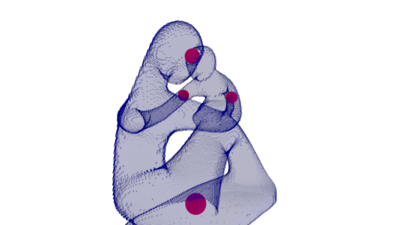
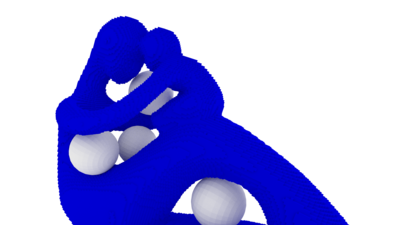
Note that there are four 1-holes instead of five.
Elephant

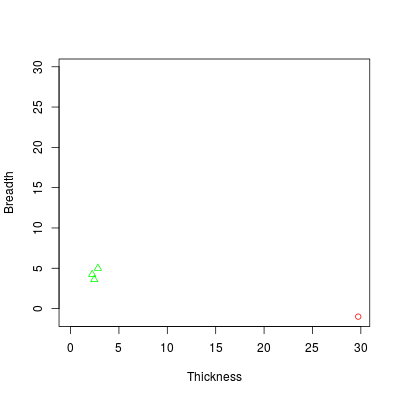
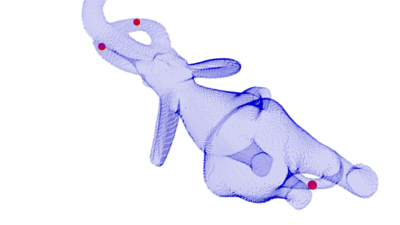

The 1-holes are small (in thickness and in breadth) with regards to the volume (0-hole).
Menger sponge
The Menger sponge is a fractal curve (!) that fits very well in this context. The model was created with this program, and it can be converted to the obj format with this. I show you the Menger sponge at different iterations, together with the thickness-breadth diagrams and some images. Note that the size of the volume is not constant: at iteration n it has size 3n. Note that I only display the "new" holes at each iteration.
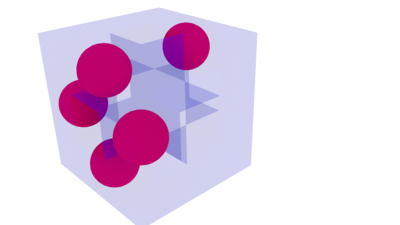

There are 5 1-holes with values (1,1).
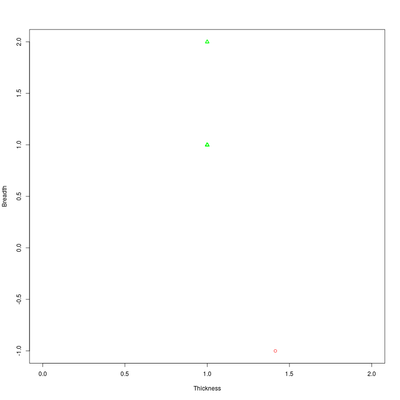


There are 5 1-holes with measures (1,2) and 76 with (1,2).
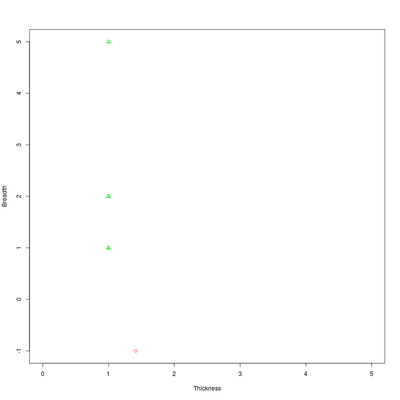


There are 5 1-holes with measures (1,5), 76 with (1,2) and 1328 with (1,1).
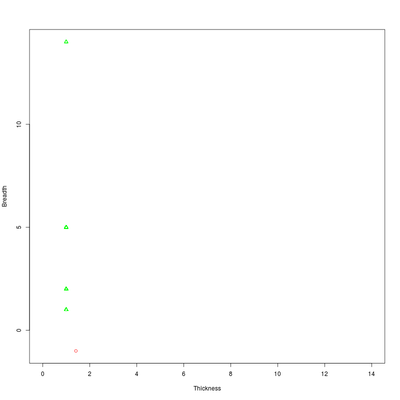
There are 5 1-holes with values (1,14), 76 with (1,5), 1328 with (1,2) and 25024 with (1,1).
The conjecture is easy to state: the Menger sponge at iteration n has 1-holes with measures ( 1, (3i+1+1)/2 ) for i = 0, ..., n. The number of 1-holes with each measure can be deducted from the formula for the number of holes in the Menger sponge.