Exercice 1 : Multiple inheritance 
Let A, B, C, D be four classes. We wish to emulate in Java the fact that D inherits from A, B and C.
Question:
Propose a UML solution for this. Which design pattern would you use?
Exercice 2 : Technical control 
Our company’s engineer has developed a control software program based on the UML diagram below. The idea is as follows: a Streamer class manages a data flow. This data is processed by a ProcessingUnit class, which can execute its computations either on GPU (CUDA) or on CPU. The processed data can be displayed by the control center via the displayProcessing() method.
More precisely, when it is constructed, the ControlCenter executes a timedProcess() thread that wakes up every 15ms to ask the ProcessingUnit it contains whether there has been an update of the data. In this case, the data is processed by the getProcessingUpdate() method and displayed via the displayProcessing() method. This process is not optimal, as updates tend to appear every 2 or 3 seconds, but, still, the software works correctly.
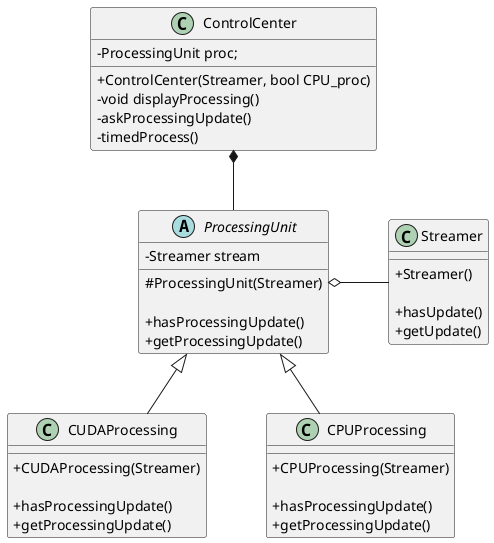
Question:
You have been recently hired in the company and you are asked to update this UML diagram in order to make it SOLID and efficient. Taking advantage of design patterns, what new UML schema would you propose?
Exercice 3 : Java's tensors 

A tensor is the computer representation of a multidimensional table. It is therefore a generalization of a vector (1-dimensional table) and of a matrix (2-dimensional table). For example, Python’s numpy arrays are tensors.
Example 1 :
Below, Tens is a tensor. Suppose its dimensions correspond to some variables x,y,z (in that order). Then Tens[0,2,1] = Tens[x=0,y=2,z=1] = 2.
| x=0 | x=1 | ||||||
|---|---|---|---|---|---|---|---|
| Tens = | y=0 | y=1 | y=2 | y=0 | y=1 | y=2 | |
| 3 | 1 | 7 | 4 | 6 | 5 | z=0 | |
| 8 | 7 | 2 | 3 | 5 | 8 | z=1 | |
Here, we wish to develop a generic Java class Tensor<T> equivalent to numpy arrays and containing elements of type T. In addition to one or more constructors, the only public methods of this class are:
int[] shape(): returns the tensor’s dimensions, as in numpy
Example :
In Example 1, Tens.shape() would return [2,3,2]. In other words, this is the number of possible values for x,y,z.
void reshape(int[]): changes the dimensions of the tensor, as in numpy
Example :
If we apply Tens.reshape([2,6]) to the tensor of Example 1, we obtain Tensor Tens_bis as shown below. In other words, Tens’s values are assigned to Tens_bis by parsing them from left to right and from top to bottom.
x=0 x=1 3 1 z=0 Tens_bis = 7 4 z=1 6 5 z=2 8 7 z=3 2 3 z=4 5 8 z=5 T get(int[] pos): returns the value of the element of the tensor at the position passed as argument
Example :
In example 1, Tens.get([0,2,1]) would return Value 2.
void set(int[] pos, T val): assigns the value val to the element of the tensor at position pos
Tensor<T> add(Tensor<T> x): calculates and returns the tensor obtained by adding the tensor x to this
Example :
If we call Tens.add(T2), with T2 defined by:
x=0 x=1 T2 = y=0 y=1 y=2 y=0 y=1 y=2 1 1 1 1 1 1 z=0 1 1 1 1 1 1 z=1 then we get the following tensor (each cell of Tens is incremented by 1):
x=0 x=1 T3 = y=0 y=1 y=2 y=0 y=1 y=2 4 2 8 5 7 6 z=0 9 8 3 4 6 9 z=1
The idea behind numpy’s multidimensional arrays (tensors) is to store all the elements internally into a vector (a MyArray<T>) and use shape information to access the elements.
In this exercise, we wish to extend this storage by proposing 2 storage methods:
classic vectors of type MyArray<T> storing all the elements;
sparse vectors MySparseArray<T>, that store only the elements differing from a certain certain value.
The elements of these two types of vectors can only be accessed via indices (position from the beginning of the vector), which are integers. For example, array[5] corresponds to the 6th element of the vector (as in a conventional array).
The add(x) and mult(x) methods of the Tensor<T> class produce new tensors. If the internal storage of the tensor x is identical to that of this, then we want the tensor they return to have the same type of internal storage (e.g. if this and x use MySparseArray<T>, the result tensors will also use MySparseArray<T>). Otherwise it must be a MyArray<T>.
Attention: you don’t want to expose the storage type outside the Tensor class. In other words, the tensor class you have to design is Tensor<T>.
Question:
Write a UML diagram to model the tensors described above, as well as the storage classes. You must enforce SOLID principles and write down the attributes of your classes as well as their methods (specifying their parameters and return types).
