Recherche textuelle

Algorithmique du texte

• modifier la casse du texte : passer un texte en majuscule, ajouter des majuscules en début de mot…
• calculer le diff entre deux textes ou aligner deux textes (par exemple des séquences de gène, ce qui est très utile en génétique)
• compter des nombres de mots dans un texte ou autres statistiques liées au texte
• rechercher un mot dans un texte

Recherche d’un motif dans un texte

• Texte stocké dans une chaîne \(T=T[0]T[1]\cdots T[n-1]\) de longueur \(n\)
• Motif à rechercher dans une chaîne \(M=M[0]M[1]\cdots M[m-1]\) de longueur \(m\leq n\)
• Le motif \(M\) apparaît à la position \(p\) dans le texte \(T\) si \(T[p+i] = M[i]\) pour tout \(0\leq i\leq m-1\)
• La recherche de motif consiste à trouver une ou toutes les positions où apparaît le motif dans le texte

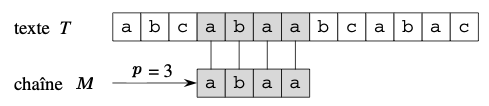
Algorithme naïf

• Tester si \(M = T[p..p+m-1]\) pour toutes les positions \(0\leq p\leq n-m\)

Cas où tous les caractères du motif \(M\) sont différents

• Comment améliorer l’algorithme naïf dans ce cas ?

Cas général : inspecter chaque lettre du texte au plus une fois ?

Utilisation d’automates finis : un automate est la donnée

• d’un ensemble \(Q\) fini d’états
• d’un état initial \(q_0\in Q\)
• d’un ensemble distingué d’états acceptants \(A\subseteq Q\) (représenté en noir ci-dessous)
• d’un alphabet fini \(\Sigma\)
• d’une fonction de transition \(\delta\colon Q\times \Sigma\to Q\)

Sémantique d’un automate fini

Sémantique :

• on démarre en \(q_0\)
• on lit un caractère \(a\in \Sigma\) et on se dirige vers l’état \(\delta(q_0,a)\)
• on continue à lire des caractères à partir de l’état courant
• à chaque fois que l’état courant appartient à \(A\), on dit que l’automate a accepté la chaîne lue jusqu’à cet endroit

\[0\xrightarrow{a} 1\xrightarrow{b}0\xrightarrow{b}0\xrightarrow{a}1\xrightarrow{a} 0\]

• \(abbaa\) rejeté
• \(abba\) accepté

Automate de recherche de motif

Exemple : motif \(ababaca\)

(les flèches manquantes vont vers l’état 0)

Complexité ?

• Une fois précalculé la fonction de transition de l’automate,
• suivre l’exécution de l’automate sur le texte demande de l’ordre de \(O(n)\) opérations

Calcul de la fonction de transition ?

• Faisable en \(O(m^3|\Sigma|)\), mais on se contentera ici de savoir le faire à la main
• Au mieux, on peut y arriver en \(O(m|\Sigma|)\), en adoptant des techniques proches d’un autre algorithme, dû à Knuth-Morris-Pratt
• L’algorithme de Knuth-Morris-Pratt évite même totalement le pré-calcul de la fonction de transition : temps de prétraitement limité à \(O(m)\), pertinent pour des gros alphabets

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…

CGGCTC
ATAACAGGAGTAAATAACGGCTCGAGTAAATA

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…

 CGGCTC
ATAACAGGAGTAAATAACGGCTCGAGTAAATA

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…

  CGGCTC
ATAACAGGAGTAAATAACGGCTCGAGTAAATA

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…

   CGGCTC
ATAACAGGAGTAAATAACGGCTCGAGTAAATA

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…
• … mais on teste l’alignement du motif sur le texte en partant de la droite du motif
• Décalage optimisé :
  • pas de A dans le motif
  • on saute directement à la position courante + 6 (longueur du motif)

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…
• … mais on teste l’alignement du motif sur le texte en partant de la droite du motif
• Décalage optimisé :
  • pas de A dans le motif
  • on saute directement à la position courante + 6 (longueur du motif)

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…
• … mais on teste l’alignement du motif sur le texte en partant de la droite du motif
• Décalage optimisé :
  • il existe un autre C dans le motif
  • on saute directement à ce C

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…
• … mais on teste l’alignement du motif sur le texte en partant de la droite du motif
• Décalage optimisé :
  • il existe un autre G dans le motif
  • on saute directement à ce G

Algorithme de Boyer-Moore

• Plus rapide des algorithmes connus
• Retour sur le glissé du motif sur le texte, utilisé dans l’algorithme naïf
• On glisse le motif de gauche à droite…
• … mais on teste l’alignement du motif sur le texte en partant de la droite du motif

Version simple : algorithme de Boyer-Moore-Horspool

• On compare le motif \(M\) avec un facteur \(T[p..p+m-1]\) du texte
• Si une différence entre \(M\) et ce facteur est constatée (ou si on a trouvé une occurrence du motif mais qu’on les veut toutes), on décale le motif vers la droite de manière à faire coïncider la dernière lettre du facteur, c’est-à-dire la lettre \(T[p+m-1]\), avec son occurrence la plus à droite dans \(M\)

Complexité ?

• Première remarque : premier algorithme qui ne lit pas nécessairement tous les caractères du texte !
• Complexité dans le pire des cas \(O(nm)\)
• En pratique (plus précisément, en moyenne sur des motifs aléatoires), l’algorithme de Horspool effectue un nombre de comparaisons de l’ordre de \(O\left(\frac n m + \frac n {2|\Sigma|}\right)\)