-
Cours :
- Arbres binaires de recherche
- cours 1
transparents : pdf, html - planche de TD/TP 1 (pdf)
- cours 1
- Tas
- cours 2
transparents : pdf, html - planche de TD/TP 2 (pdf)
- cours 2
- Parcours de graphe
- cours 3
transparents : pdf, html - planche de TD/TP 3 (pdf)
- cours 3
- Plus courts chemins et coloration de graphe
- cours 4
transparents : pdf, html - planche de TD/TP 4 (pdf)
- cours 4
- Programmation dynamique 1
- cours 5
transparents : pdf, html - planche de TD/TP 5 (pdf)
- cours 5
- Programmation dynamique 2
- Recherche textuelle
- cours 7
transparents : pdf, html - planche de TD/TP 7 (pdf)
- cours 7
- Algorithmes randomisés
- cours 8
transparents : pdf, html - planche de TD/TP 8 (pdf)
- cours 8
- Calculabilité
- transparents : pdf
- planche de TD/TP 9 (pdf)
- Complexité
- transparents : pdf
- planche de TD/TP 10 (pdf)
Plus courts chemins et coloration de graphe
Algorithme de Dijkstra
Soit \((G = (S,A), w)\) un graphe pondéré avec des poids positifs ou nuls, \(w\colon A\to \mathbf N\) donnant le poids de chaque arc. L’algorithme de Dijkstra est un algorithme glouton, qui utilise une file de priorité minimum \(F\), dont les clés sont les sommets \(u\) du graphe, associées à la priorité \(d[u]\):
Pour u dans S :
d(u) = infini
pi(u) = nil
d(s) = 0
F = file(S)
Tant que F est non vide :
u = extraire_minimum(F)
Pour chaque sommet v adjacent à u :
relâcher(u,v,w)où la fonction relâcher est donnée ci-dessous:
fonction relacher(u, v, poids_arc):
si d(v) > d(u) + poids_arc(u,v)
alors d(v) = d(u) + poids_arc(u,v); pi(v) = uQuestion 1 Exécuter cet algorithme sur le graphe suivant :
Question 2 Montrer qu’à la fin de l’exécution de l’algorithme, pour tout sommet \(u\in S\), \(d(u)=\delta(s,u)\). Pour ce faire, on pourra employer l’invariant de boucle : au début de chaque itération de la boucle Tant que, pour chaque sommet \(v\) qui n’apparaît plus dans la file de priorité \(F\), \(d(v)=\delta(s,v)\).
Question 3 On a vu dans les séances précédentes comment implémenter une file de priorité minimum avec un tas. Mais il y a d’autres implémentations plus simples à mettre en œuvre. Expliquer comment on peut représenter une file de priorité min à l’aide d’un dictionnaire associant à chaque clé sa priorité et la complexité des différentes opérations dans ce cas.
Question 4 L’algorithme relâcher nécessite de mettre à jour la priorité d’une clé avec une valeur inférieure. Comment implémenter cette opération dans les deux représentations des files de priorité minimum ?
Question 5 Étudier la complexité de l’algorithme de Dijkstra, selon le choix d’implémentation de la file de priorité min. Donner une condition sur le graphe \(G\) pour que l’utilisation des tas min soit profitable.
Question 6 Utiliser l’implémentation de file de priorité minimum à l’aide de tas, pour proposer une implémentation de l’algorithme de Dijkstra.
Question 7 Tester votre algorithme avec le graphe ci-dessus.
Piste d’activités Utiliser des données d’OpenStreetMap pour travailler sur des graphes modélisant un réseau routier… cf le projet pyroutelib3 par exemple, qu’on peut même utiliser dès SNT https://pixees.fr/informatiquelycee/n_site/snt_carto_route.html
Graphes pondérés avec des poids négatifs
Jusque-là, nous avons étudié uniquement des graphes pondérés avec des poids entiers positifs ou nuls : pourtant, on pourrait imaginer des graphes avec des poids négatifs, par exemple si le poids de l’arc représente des échanges d’argent (vente ou achat de produits).
Question 8 Exécuter l’algorithme de Dijkstra sur l’exemple ci-dessous où plusieurs arcs ont des poids négatifs :
Question 9 Qu’en déduire sur l’algorithme de Dijkstra?
Piste d’activités Il existe bien évidemment d’autres algorithmes pour les graphes à poids positifs et négatifs, l’algorithme de Bellman-Ford par exemple.
Coloration de graphes
Les graphes ont de nombreuses applications qu’on a déjà vues. L’une d’elle est utile pour le calcul sur des représentations de cartes. Imaginons la tâche d’un géographe qui souhaite colorier les pays d’une carte du monde avec le moins de couleurs possibles, tout en garantissant toujours que deux pays partageant une frontière terrestre n’ont pas la même couleur. Après un peu de tâtonnement, le géographe s’aperçoit qu’il arrive toujours à colorer ses mappemondes avec quatre couleurs. Est-ce un hasard ? En fait, non, c’est toujours possible comme le dit le théorème des quatre couleurs:
Question 10 Modéliser ce problème en terme de graphe et définir une notion de coloration de graphe permettant de poser le problème. Quelle propriété (qu’on appelle planaire) ont alors les graphes provenant des cartes géographiques? Donner un exemple de graphe qui n’est pas le graphe d’une carte.
Le théorème des quatre couleurs a une grosse lacune: il dit qu’il est possible de colorer les pays d’une carte (ou les sommets d’un graphe planaire) avec quatre couleurs, mais ne donne pas de méthode pour faire cela. Comment donc colorer effectivement un graphe planaire, ou une carte de géographie, à partir de là?
Question 11 Une première méthode naïve pourrait consister à essayer toutes les possibilités de coloriage, jusqu’à en avoir trouvé une correcte. Donner une majoration de la complexité dans le pire des cas d’un tel algorithme d’énumération.
Question 12 Une méthode plus efficace consiste à utiliser l’algorithme de Welsh-Powell qu’on peut écrire de la manière suivante:Appliquer cet algorithme au graphe ci-dessous.
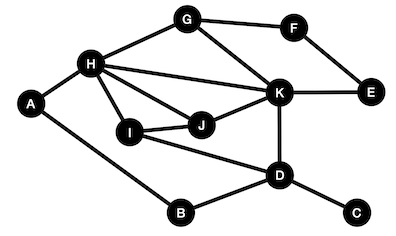
Donne-t-il une coloration optimale en terme du nombre de couleurs?
Question 13 Trouver un exemple de graphe où l’algorithme de Welsh-Powell ne fournit pas une coloration optimale. En particulier, même sur un graphe planaire, il ne fournit pas nécessairement une coloration utilisant au plus 4 couleurs… C’est en fait un problème compliqué de trouver le nombre minimal de coloration nécessaire pour colorer un graphe: c’est un problème NP-complet (ce qu’on rediscutera d’ici la fin du bloc 5).