-
Cours :
- Arbres binaires de recherche
- cours 1
transparents : pdf, html - planche de TD/TP 1 (pdf)
- cours 1
- Tas
- cours 2
transparents : pdf, html - planche de TD/TP 2 (pdf)
- cours 2
- Parcours de graphe
- cours 3
transparents : pdf, html - planche de TD/TP 3 (pdf)
- cours 3
- Plus courts chemins et coloration de graphe
- cours 4
transparents : pdf, html - planche de TD/TP 4 (pdf)
- cours 4
- Programmation dynamique 1
- cours 5
transparents : pdf, html - planche de TD/TP 5 (pdf)
- cours 5
- Programmation dynamique 2
- Recherche textuelle
- cours 7
transparents : pdf, html - planche de TD/TP 7 (pdf)
- cours 7
- Algorithmes randomisés
- cours 8
transparents : pdf, html - planche de TD/TP 8 (pdf)
- cours 8
- Calculabilité
- transparents : pdf
- planche de TD/TP 9 (pdf)
- Complexité
- transparents : pdf
- planche de TD/TP 10 (pdf)
Files de priorité et tas
Files de priorité
Les piles et les files sont des structures de données permettant de traiter des objets dans un ordre dépendant uniquement de leur insertion dans la structure. Les files de priorité assouplissent ce mécanisme en équipant chaque objet d’une priorité (modifiable), à la façon d’une caisse de supermaché dans laquelle les femmes enceintes sont prioritaires. On va supposer ici qu’on considère une file de priorité minimum, c’est-à-dire que l’objet le plus prioritaire est celui dont la priorité est minimale (il existe une variante maximale également, tout à fait symétrique).
Étudions une implémentation possible de telles files de priorité minimum à l’aide de tas. Un tas est un arbre binaire parfait étiqueté par les priorités (on oublie désormais que les priorités sont rattachées à des objets pour ne se concentrer que sur les priorités elles-même) tel que pour tout nœud \(p\) d’étiquette \(x\), toutes les étiquettes des enfants de \(p\) sont supérieures à \(x\). Parfait signifie que tous les niveaux sont complets, sauf le dernier rempli de gauche à droite. Voici un exemple de tas:
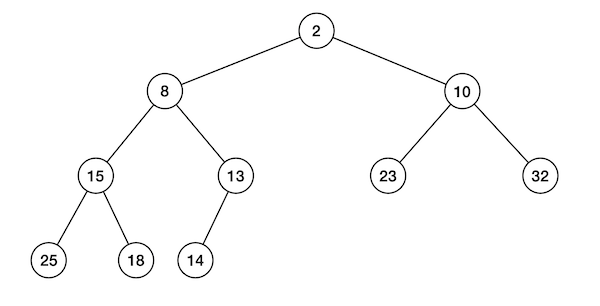
On pourrait choisir d’encoder un tas à l’aide des structures d’arbres binaires qu’on a déjà étudiées, mais un autre encodage est souvent préféré, à l’aide de tableaux. On associe à chaque tas le tableau de ces éléments dans l’ordre d’un parcours en largeur de gauche à droite (c’est-à-dire qu’on lit les étiquettes niveau par niveau de gauche à droite). Par exemple, on utilise le tableau \([2, 8, 10, 15, 13, 23, 32, 25, 18, 14]\) pour encoder le tas précédent.
Question 1 Quels sont les indices du tableau stockant les enfants gauche et droit, et le parent du nœud stocké dans l’indice \(i\) du tableau encodant un tas?
Question 2 Quels sont les indices du tableau stockant des feuilles du tas?
Question 3 En déduire l’implémentation d’une classe MinimumHeap, avec un constructeur permettant d’initialiser un tas vide et avec des méthodes is_empty et minimum pour tester si le tas est vide et retourner le minimum du tas (si le tas est non vide), respectivement. Ajouter des méthodes (qu’il faut imaginer privées) permettant de tester si un indice passé en argument est une feuille du tas, et d’accéder à l’indice de l’enfant gauche, de l’enfant droit et du parent d’un indice passé en argument.
Question 4 Ajouter (à la main) successivement les priorités 22, 9, 1, 31, 11 et 24 dans le tas précédent.
Question 5 Ajouter une méthode insert qui ajoute au tas une nouvelle priorité donnée en argument. Il pourra être utile de commencer par implémenter une méthode heapify (entasser en français) qui prend en argument un nœud \(x\) de l’arbre binaire dont les deux enfants sont des tas mais qui n’est pas un tas uniquement à cause de la contrainte non vérifiée à la racine du sous-arbre (la priorité au nœud \(x\) est supérieure strictement à au moins l’une des deux priorités des deux enfants), et qui modifie l’arbre pour le transformer en un tas contenant le même ensemble de priorité.
Question 6 Ajouter une méthode extract_minimum qui renvoie la priorité minimale et la supprime du tas.
Tri par tas
On peut utiliser des tas pour réaliser un tri d’une liste. Pour cela, on insère successivement les éléments de la liste à trier, puis on extrait le minimum successivement qu’on stocke à nouveau dans la liste jusqu’à obtenir un tas vide.
Question 7 Proposer une fonction qui trie une liste donnée en argument à l’aide de tas.
Question 8 Estimer la complexité de cet algorithme, en termes de nombre de comparaisons d’éléments de la liste, en fonction de la longueur \(n\) de la liste.
Files de priorité fusionnables
Une extension parfois bien utile des files de priorité consiste à pouvoir fusionner des files de priorité: dans l’analogie des files d’attente aux caisses d’un supermarché, c’est l’opération qui doit être effectuée lorsqu’une caisse ferme alors qu’il y avait encore des clients patientant dans la file…
Question 9 Proposer une solution simple pour fusionner deux tas à l’aide des outils connus jusqu’à maintenant: on s’attend à trouver un algorithme de complexité \(O(n\log n)\) si \(n\) est le nombre total de priorités dans les deux tas.
Pour faire mieux, on va changer de modèle, et considérer non plus des tas qui sont des arbres binaires parfaits, mais des tas gauches. Dans un arbre binaire, on appelle branche droite la liste des nœuds obtenus en suivant les enfants droits à partir de la racine. Le rang droit d’un nœud d’un arbre binaire est la longueur de la branche droite issue de ce nœud. Un arbre gauche est un arbre binaire tel que pour chaque nœud le rang droit de son enfant gauche est supérieur ou égal au rang droit de son enfant droit. Un tas gauche est un arbre gauche étiqueté par des priorités qui garantit en plus la propriété de tas, à savoir que la priorité d’un nœud est toujours inférieure aux priorités de ses enfants.
Question 10 Les arbres suivants sont-ils des arbres gauches? Si oui, complétez les étiquettes des nœuds avec des entiers cohérents avec la propriété de tas minimum, afin d’obtenir un tas gauche.
Question 11 Montrer que tout tas gauche à \(n\) éléments a un rang droit au plus \(\log_2 (n+1)-1\).
Question 12 Expliquer comment on peut produire un tas à partir de deux tas gauches et d’une priorité inférieure à toutes celles des deux tas. Assurez-vous que le tas renvoyé vérifie bien tous les invariants d’un tas gauche!
Question 13 En déduire un algorithme récursif pour fusionner deux tas gauches. L’appliquer aux tas gauches ci-dessous:
Question 14 Quelle est la complexité de cet algorithme de fusion de tas gauches?
Question 15 Proposer alors des fonctions permettant de réaliser l’insertion d’une nouvelle priorité dans un tas gauche et l’extraction de la priorité minimum. Calculer leur complexité.