Structures de données : arbres
Benjamin Monmege
Exemples d’utilisation des arbres
Arbre syntaxique d’une expression arithmétique
Arbre syntaxique analysant une phrase
Arbre généalogique
Arbre lexicographique (ou en parties communes, ou dictionnaire)
Arbre de décision
Arbre de versions git
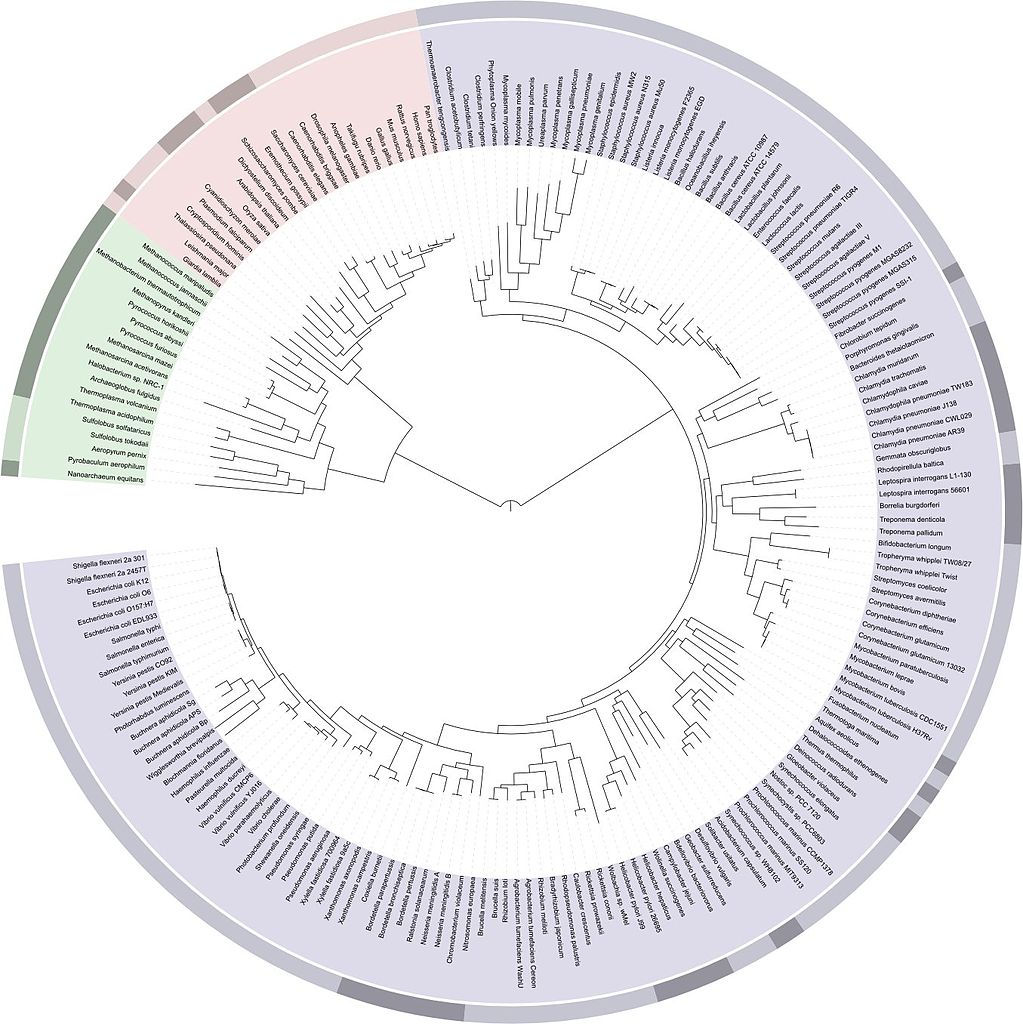
Arbre phylogénétique
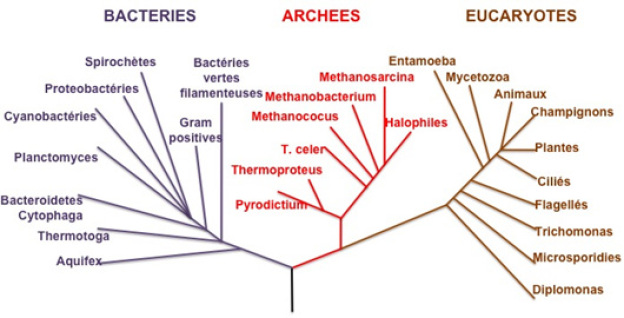
Arbre phylogénétique
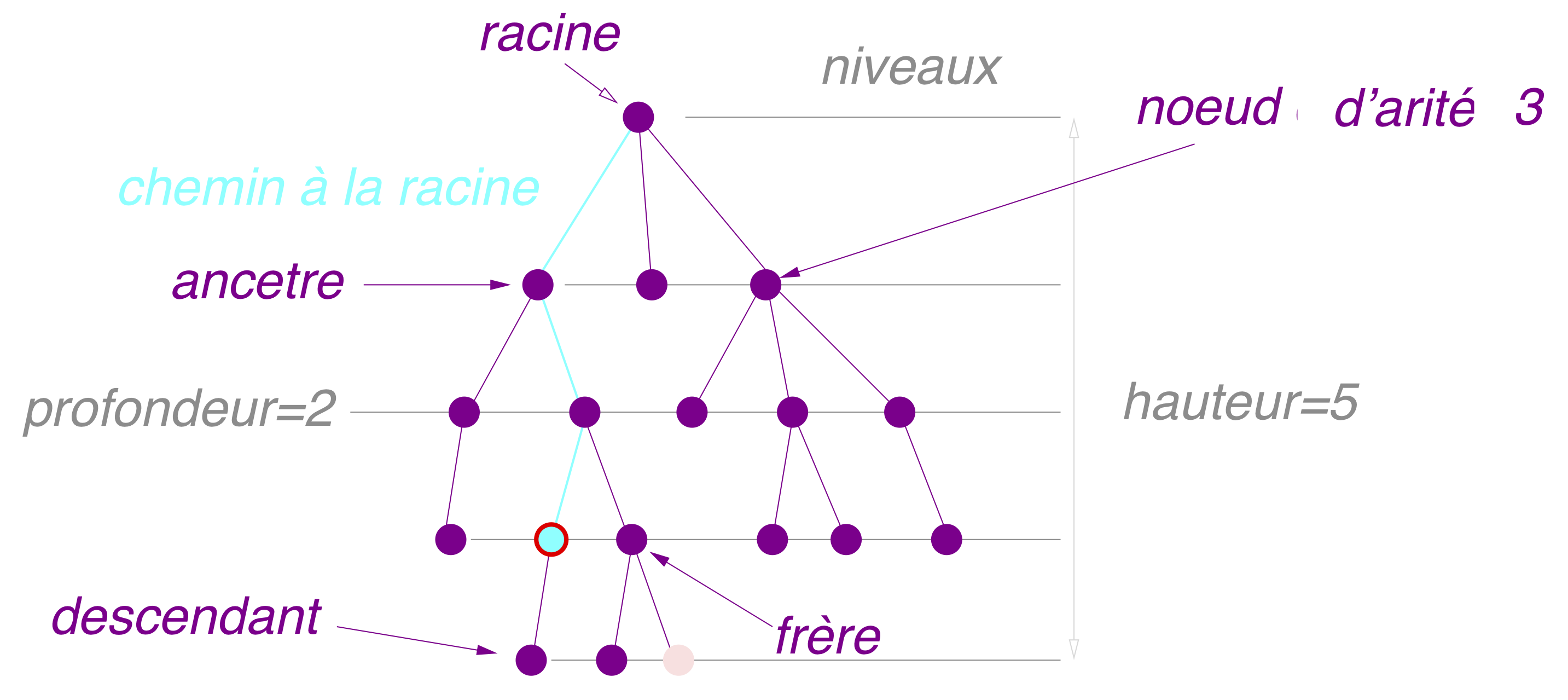
Définitions d’un arbre enraciné
Définition ensembliste
Un arbre est un ensemble organisé de nœuds :
- chaque nœud a un unique parent,
- sauf un seul nœud, la racine, qui n’a pas de parent.
Les nœuds ayant un nœud \(p\) comme parent sont appelés les enfants de \(p\).
Les feuilles sont les nœuds qui n’ont pas d’enfants.
Définition récursive
Un arbre est constitué :
- d’un nœud \(p\), sa racine,
- et d’une suite de sous-arbres \((a_1,a_2,\ldots,a_k)\) (avec \(k\) non fixé a priori).
Les racines des arbres \(a_1,a_2,\ldots,a_k\) sont les enfants de \(p\).
Les mots des arbres
Parcours
Parcourir un arbre (ou un graphe…), c’est visiter la totalité des nœuds de celui-ci, dans un certain ordre, pour appliquer un éventuel traitement: affichage, évaluation, recherche…
Parcours en profondeur
Parcours en largeur
Arbres binaires
Définition
Chaque nœud a au plus 2 enfants : l’enfant gauche et l’enfant droit
Hauteur et taille d’un arbre binaire
Arbre binaire complet de hauteur \(h\) (hauteur = nombre de niveaux):
- à la profondeur \(p\) on a \(2^{p}\) nœuds
- le nombre total de nœuds est donc \(\Sigma_{i=0}^{h-1} 2^{i} = 2^{h}-1\)
Un arbre quelconque de hauteur \(h\) contient au plus \(2^h-1\) nœuds.
Parcours en profondeur d’un arbre binaire
Parcours préfixe : traitement du nœud avant les sous-arbres
Parcours infixe : traitement du nœud entre les deux sous-arbres
Parcours postfixe : traitement du nœud après les sous-arbres
Structure de données abstraite : ensemble dynamique
Structure de données abstraite : ensemble dynamique
- Recherche d’un élément dans un ensemble
- Insertion d’un nouvel élément
- Suppression d’un élément
- Test du vide de l’ensemble
Interface :
Première implémentation : liste triée dans le cas où les éléments sont comparables
- Recherche d’un élément dans un ensemble: recherche dichotomique
\(O(\log(n))\)
- Insertion d’un nouvel élément: recherche puis décalage
\(O(n)\)
- Suppression d’un élément: recherche puis décalage
\(O(n)\)
- Test du vide de l’ensemble: test de longueur
\(O(1)\)
Seconde implémentation : arbre binaire de recherche dans le cas où les éléments sont comparables
Arbre binaire étiqueté par les éléments tel que pour tout nœud \(p\) d’étiquette \(x\):
- toutes les étiquettes de l’enfant gauche de \(p\) sont inférieures à \(x\)
- toutes les étiquettes de l’enfant droit de \(p\) sont supérieures à \(x\)
Algorithmes et complexité: bloc 5 !
Troisième implémentation : table de hachage dans le cas d’éléments hachables
Principe :
- appliquer une fonction de hachage (ou dispersion) permettant d’associer à chaque élément un indice \(i\) dans un intervalle restreint de valeurs
- ranger l’élément dans la case d’indice \(i\) d’une liste (appelée table de hachage)
- en cas de collision (deux éléments à insérer de même fonction de hachage), on stocke une liste d’éléments dans la case d’indice \(i\)
Structures utilisée pour les dictionnaires Python