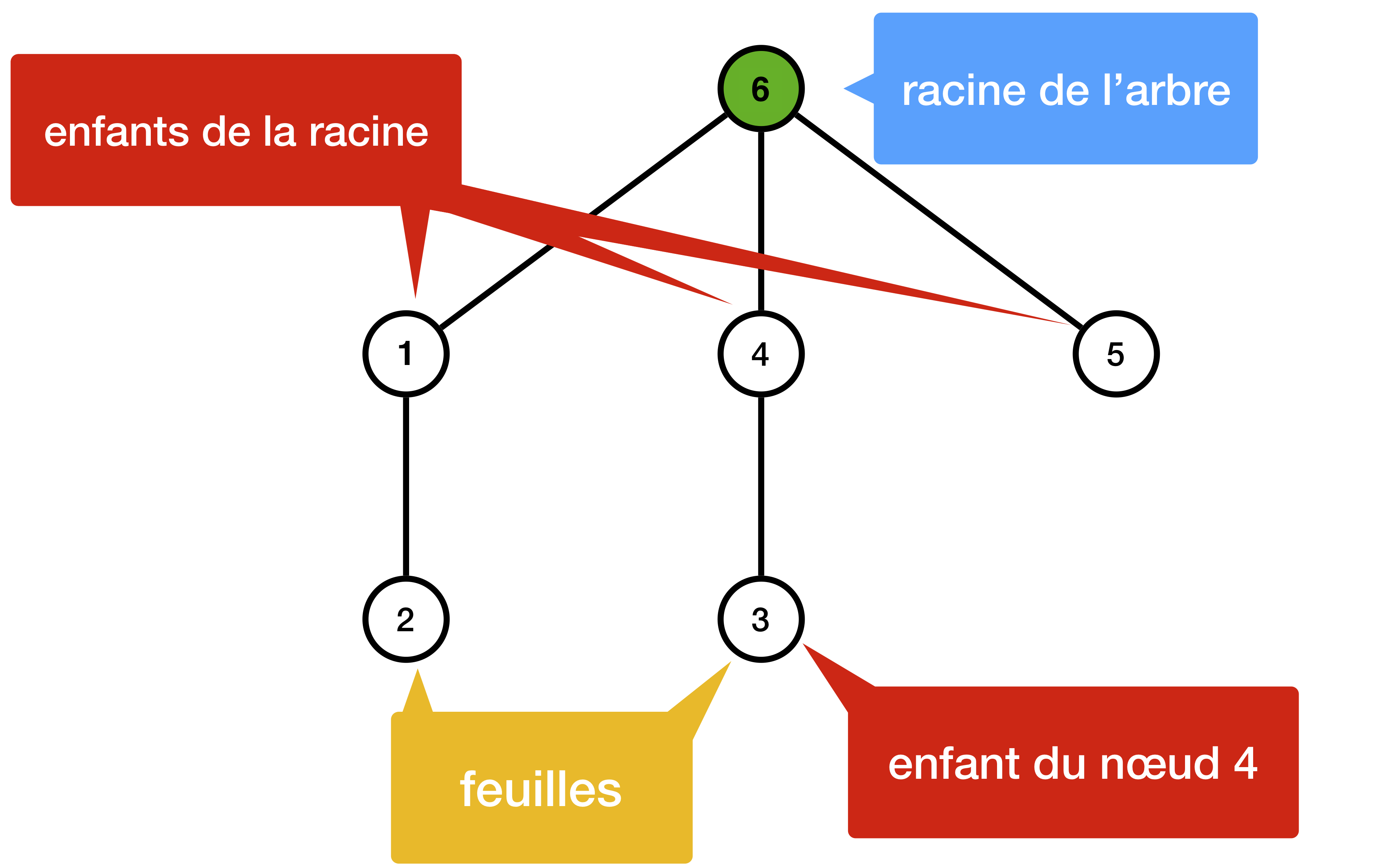
Structures de données : graphes
Benjamin Monmege
Exemples d’utilisation des graphes
Réseau routier
Réseau routier : avec sens interdits
Internet
Réseaux sociaux

Jeux : graphe des configurations
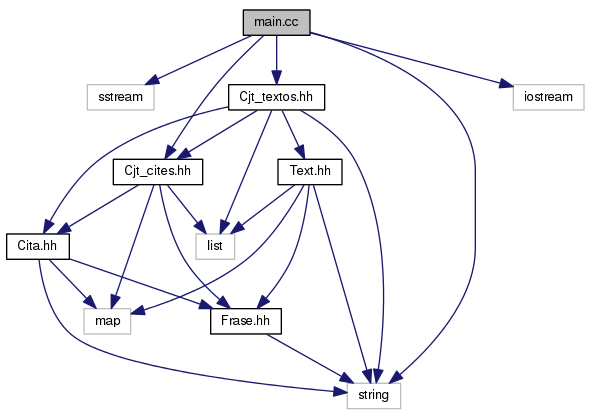
Graphe de dépendances
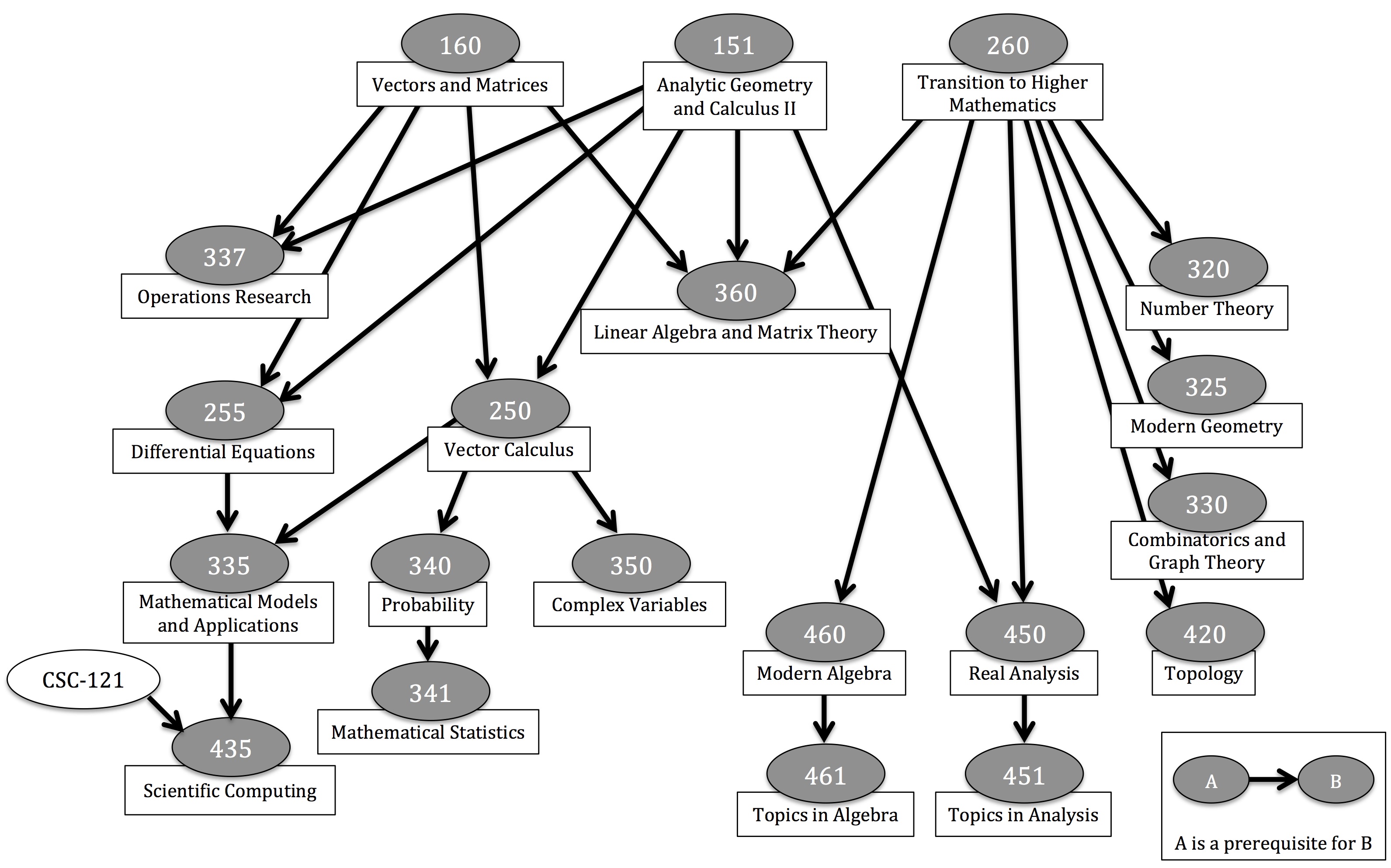
Graphe de prérequis
Définition d’un graphe
Graphe orienté
Un graphe orienté est la donnée :
d’un ensemble \(S\) de sommets
et d’un ensemble \(A\) d’arcs, chaque arc étant un couple \((u,v)\) de deux sommets (possiblement les deux mêmes), parfois noté \(u\to v\) : \(u\) est la source de l’arc et \(v\) sa destination
Un chemin est une suite de sommets \(u_0,u_1,\ldots,u_k\) (avec \(k\geq 0\)) reliés par des arcs, c’est-à-dire telle que \(u_i\to u_{i+1}\) pour tout \(i\in \{0,\ldots,k-1\}\).
Relation
Un graphe orienté permet de représenter une relation entre des éléments d’un ensemble fini :
- relation de parenté
- relation d’amitié (pas forcément réciproque)
- relation d’ordre sur l’âge…
Graphe non orienté
Si les flèches ne sont pas importantes pour modéliser le problème, on utilise plutôt un graphe non orienté :
- il est composé d’un ensemble \(A\) d’arêtes, chaque arête étant une paire \(\{u,v\}\) de deux sommets distincts.
On parle alors de chaîne plutôt que de chemin.
Représentation d’un graphe
Matrice d’adjacence
Liste de successeurs : dictionnaire Python
Il existe aussi une représentation par liste de prédécesseurs: il faut choisir la meilleure des représentations selon le problème à résoudre sur les graphes…
Arbre comme sous-graphe
Connexité
- Une composante connexe d’un graphe non orienté est un ensemble maximal de sommets tous reliés les uns aux autres par un chemin.
- Un graphe peut se décomposer de manière unique en un ensemble de composantes connexes.
- Un graphe est dit connexe s’il ne possède qu’une unique composante connexe.
Une notion similaire existe pour les graphes orientés : la forte connexité
Acyclicité
- Un circuit dans un graphe non orienté est une chaîne partant et arrivant dans le même sommet. On parle de cycle dans un graphe orienté.
- Un graphe est dit acyclique s’il ne possède aucun circuit/cycle.
Caractérisation des arbres
Tout graphe connexe et acyclique est un arbre…
… au sens où on peut choisir n’importe quel sommet comme racine et obtenir un arbre d’arité non borné en considérant ses voisins, puis les voisins de ses voisins, etc.