-
Cours :
- Bases de données 1
- Bases de données 2
- Bases de données 3
- Bases de données 4
- Bases de données 5
- Programmation orientée objet
- cours 6
transparents : pdf, html - planche de TD/TP 6 (pdf)
- cours 6
- Programmation évènementielle
- Structures de données : listes, piles, files
- cours 8
transparents : pdf, html - planche de TD/TP 8 (pdf)
- cours 8
- Structures de données : arbres et ABR
- cours 9
transparents : pdf, html - planche de TD/TP 9 (pdf)
- cours 9
- Structures de données : graphes
- cours 10
transparents : pdf, html - planche de TD/TP 10 (pdf)
- cours 10
Structures de données : arbres
Arbres binaires
Commençons par étudier les arbres binaires, en utilisant une définition récursive : un arbre binaire est
- soit un arbre vide (qu’on codera par
Noneen Python) - soit un nœud ayant une étiquette, et deux arbres qu’on appelle enfant gauche et enfant droit.
On choisit d’implémenter de tels arbres binaires à l’aide de la classe suivante, où on utilise des valeurs par défaut dans le constructeur pour les deux enfants :
class BinaryTree:
def __init__(self, label, left_child=None, right_child=None):
self.label = label
self.left = left_child # None ou un arbre de la classe BinaryTree
self.right = right_child # None ou un arbre de la classe BinaryTreeQuestion 1 Utiliser cette classe pour stocker l’arbre suivant :
Question 2 Ajouter une méthode is_leaf testant si l’arbre est une feuille.
Question 3 La question du parcours de l’ensemble des nœuds d’un arbre est cruciale, en particulier pour l’affichage. Compléter la méthode __repr__ (qui sera récursive !) d’affichage de l’ensemble des informations stockées dans l’arbre qui associe par exemple à l’arbre ci-dessus la chaîne "<3,<4,<>,<2>>,<7,<6>,<5,<1>,<0>>>>":
def __repr__(self):
if self.is_leaf():
return ...
if self.left is None:
str_gauche = ...
else:
str_gauche = ...
if self.right is None:
str_droite = ...
else:
str_droite = ...
return ...Question 4 Ajouter une méthode height renvoyant la hauteur de l’arbre : attention au fait qu’un nœud peut avoir 0, 1 ou 2 enfants.
Question 5 Donner un encadrement le plus fin possible de la hauteur d’un arbre binaire possédant \(n\) nœuds.
L’affichage vu en question 3 n’est pas toujours satisfaisant, en fonction du domaine d’application des arbres. Par exemple, nous avons déjà vu que les expressions arithmétiques (sans variables) peuvent être représentées d’une manière très proche de ce que nous venons de faire pour les arbres binaires. Supposons aujourd’hui qu’on les représente directement avec un arbre binaire dont l’étiquette est un opérateur arithmétique (pour le cas d’un nœud interne) ou un nombre (pour le cas d’une feuille).
Cependant, nous avons implémenté une autre représentation des expressions, plus adaptée. Il s’agit également d’un parcours, mais imprimant l’étiquette du nœud entre l’enfant gauche et l’enfant droit (on peut ainsi modéliser des opérations unaires avec notation préfixe tel que l’opposé ou le cosinus, ou suffixe tel que le carré). On parle de parcours infixe totalement parenthésé:
def infix_traversal(self):
s = ""
if self.left is not None:
s += self.left.infix_traversal()+" "
s += str(self.label)
if self.right is not None:
s += " "+self.right.infix_traversal()
if self.is_leaf():
return s
return "("+s+")"Question 6 Tester cette méthode. La modifier en supprimant les parenthèses de la dernière ligne et trouver deux arbres simples, modélisant des expressions arithmétiques différentes, ayant alors la même représentation.
On peut cependant se passer de parenthèses, au prix d’un changement de l’ordre d’apparition des éléments de l’expression arithmétique. On parle de notation polonaise inversée, qui correspond en fait à un parcours postfixe (ou suffixe) de l’arbre binaire : on imprime l’étiquette du nœud après avoir imprimé l’enfant gauche puis l’enfant droit.
Question 7 Implémenter une méthode renvoyant la chaîne du parcours postfixe, où les étiquettes sont séparées par des espaces pour améliorer la lisibilité : par exemple, l’expression arithmétique \((5+4)\times (3-(2+1))\) s’affichera sous la forme “5 4 + 3 2 1 + - \(\times\)”.
Notez que la fonction d’évaluation que vous aviez écrite la semaine dernière ressemble de près à ce parcours postfixe : en effet, on commence par évaluer les deux sous-expressions avant d’appliquer l’opération décrite par l’étiquette du nœud.
Les calculatrices Hewlett-Packard proposaient à leurs utilisateurs d’entrer les expressions arithmétiques à calculer à l’aide de la notation polonaise inversée. Nous allons donc proposer une fonction (en dehors de la classe BinaryTree) qui reçoit une liste de symboles (plutôt qu’une chaîne de caractères comme au-dessus, pour simplifier l’écriture) et renvoie l’arbre binaire dont la liste précédente est le parcours postfixe : à partir de la liste [5, 4, “+”, 3, 2, 1, “+”, “-”, “\(\times\)”] où on utilise des chaînes de caractères pour représenter les symboles, et des entiers pour représenter les constantes, on doit reconstruire l’arbre de l’expression arithmétique \((5+4)\times (3-(2+1))\). Pour ce faire, on utilise une pile, initialement vide. On considère successivement les éléments de la chaîne de caractères :
- si c’est un entier, on l’empile;
- si c’est le symbole d’un opérateur arithmétique \(f\) (on suppose pour simplifier qu’on n’utilise que des symboles binaires désormais), alors on dépile les deux derniers éléments et on construit l’arbre d’étiquette \(f\) et d’enfants les deux sous-arbres dépilés (attention à l’ordre !), et on le rempile.
Question 8 Appliquer à la main cet algorithme à la liste [5, 4, “+”, 3, 2, 1, “+” “-” “\(\times\)”].
Question 9 En utilisant votre implémentation objet de la structure de pile, implémenter cette fonction de construction d’un arbre à partir de son parcours postfixe.
Arbres d’arité non bornée
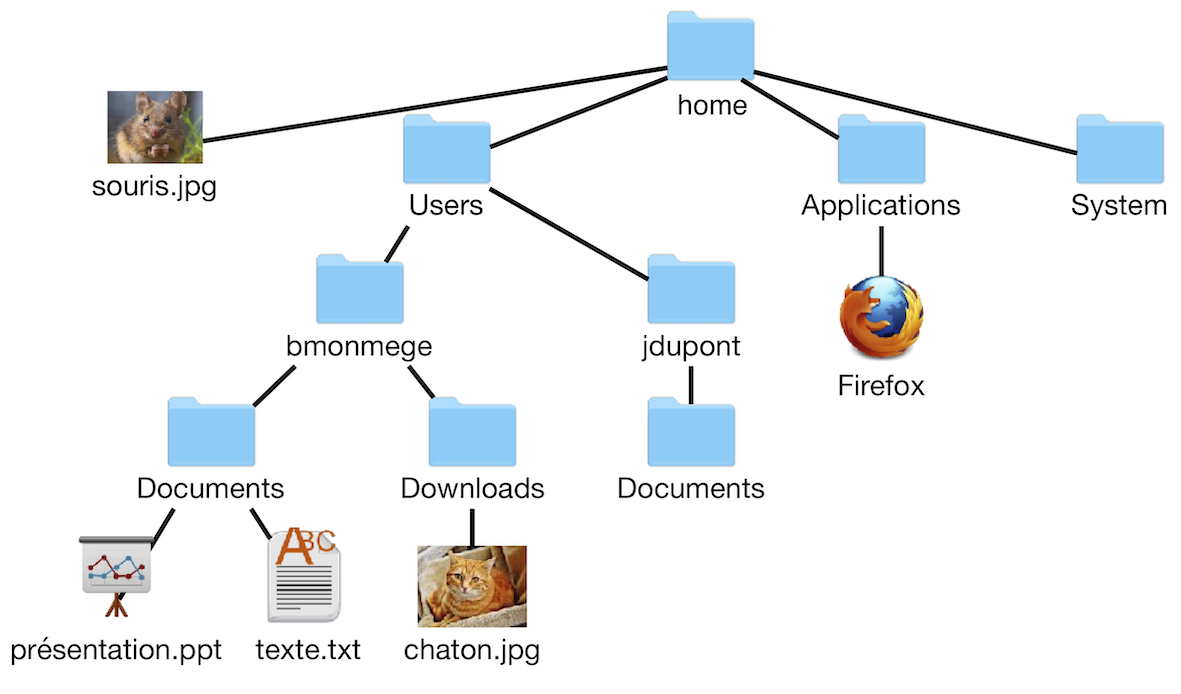
Tous les arbres ne sont pas binaires. Par exemple, si on souhaite représenter une arborescence de fichiers telle que celle représentée ci-dessus, il n’est pas opportun de se limiter à l’utilisation d’arbres binaires. On préfèrera utiliser des arbres d’arité non bornée, c’est-à-dire où chaque nœud a une étiquette, ainsi qu’une liste (ordonnée donc) d’enfants qui sont eux-mêmes des arbres d’arité non bornée. Une feuille est donc un nœud n’ayant aucun enfant.
Question 10 Implémenter une classe INode permettant de représenter les inodes d’une arborescence de fichier. Chaque inode a un attribut name pour stocker son nom (le nom du fichier ou du répertoire correspondant) et une liste d’inodes enfants (on pourra utiliser les listes Python).
Question 11 Ajouter deux classes File (pour représenter les fichiers, pas les files…) et Repository, héritant toutes les deux de la classe INode, et n’ayant que deux méthodes propres is_file et is_repository, permettant de distinguer les répertoires des autres fichiers.
On veut désormais simuler l’affichage récursif de l’ensemble des fichiers d’un répertoire donné, tel qu’on l’obtient sous Unix en tapant la commande bash ls -R. Sur l’arborescence donnée en exemple précédemment, on veut obtenir:
souris.jpg Users Applications System
home/Users:
bmonmege jdupont
home/Users/bmonmege:
Documents Downloads
home/Users/bmonmege/Documents:
présentation.ppt texte.txt
home/Users/bmonmege/Downloads:
chaton.jpg
home/Users/jdupont:
Documents
home/Users/jdupont/Documents:
home/Applications:
Firefox
home/System:Question 12 Un tel affichage correspond à un parcours préfixe de l’arborescence. Implémenter une méthode ls de la classe INode permettant d’arriver à ce résultat. On pourra utiliser le découpage en méthode
def string_of_children(self) -> str:
"""renvoie la chaîne de caractères obtenue en concaténant les noms
des enfants de l'inode, séparés par des espaces"""
def string_of_subrepositories(self, prefix:str) -> str:
"""renvoie la chaîne de caractères obtenue par un parcours préfixe
de l'arborescence où chaque nœud apparait sous la forme
prefix/path_to_node:
list_of_children
"""
def ls(self) -> str:
"""si l'inode est un répertoire, renvoie la chaîne de caractères
représentant le résultat de la commande bash ls -R"""Arbres lexicographiques
Une dernière application classique des arbres (d’arité non bornée) consiste à stocker un dictionnaire de mots. Par exemple, pour stocker la liste de mots [‘AIR’, ‘AIL’, ‘ART’, ‘AU’, ‘AUX’, ‘DE’], on utilise l’arbre lexicographique suivant:
On utilise un point à la racine de l’arbre pour pouvoir lister un ensemble de mots ne commençant pas tous par la même lettre. On utilise également le point pour signifier que le mot obtenu en concaténant les lettres jusqu’au parent est un mot du dictionnaire : dans une application pratique, on pourrait ajouter un champ definition permettant, non seulement de dire qu’un mot est dans le dictionnaire, mais aussi de donner sa définition.
Question 13 En vous inspirant de l’implémentation des inodes, proposer une implémentation des arbres lexicographiques, offrant la possibilité d’obtenir la liste des mots représentés par l’arbre.