Structures de données : graphes

Structures de données : graphes

Implémentations des graphes

On se place dans le cadre des graphes orientés décrits par un ensemble \(S\) de sommets et un ensemble \(A\) d’arcs, chaque arc étant un couple \((u,v)\) de deux sommets (possiblement les deux mêmes), parfois noté \(u\to v\).

On peut stocker des graphes orientés avec :

  • une matrice d’adjacence : c’est une matrice \(M\) carrée de booléens, indexée par les sommets du graphe, telle que \(M_{u,v}\) est vraie si et seulement s’il y a un arc \((u,v)\) de \(u\) à \(v\);
  • une liste de successeurs : c’est un dictionnaire associant à chaque sommet \(u\) la liste de ses successeurs, c’est-à-dire la liste des sommets \(v\) tels que \((u,v)\in A\).

Question 1 Coder en Python la matrice d’adjacence du graphe ci-dessous. Il sera plus facile d’utiliser la bibliothèque numpy aujourd’hui. Pour initialiser une matrice avec une certaine constante, on peut utiliser la fonction full de cette bibliothèque.


Question 2 Écrire une fonction associant à une matrice d’adjacence donnée en argument le dictionnaire représentant sa liste de successeurs.

Question 3 Écrire une fonction réciproque produisant la matrice d’adjacence à partir d’une liste d’adjacence. On pourra utiliser (après les avoir comprises) les deux lignes suivantes :

Vérifier que la matrice obtenue en appliquant les deux fonctions précédente est bien identique à la matrice d’adjacence codée initialement.

Petit monde et clôture transitive

Les graphes peuvent permettre de modéliser les relations d’amitié dans un réseau social:


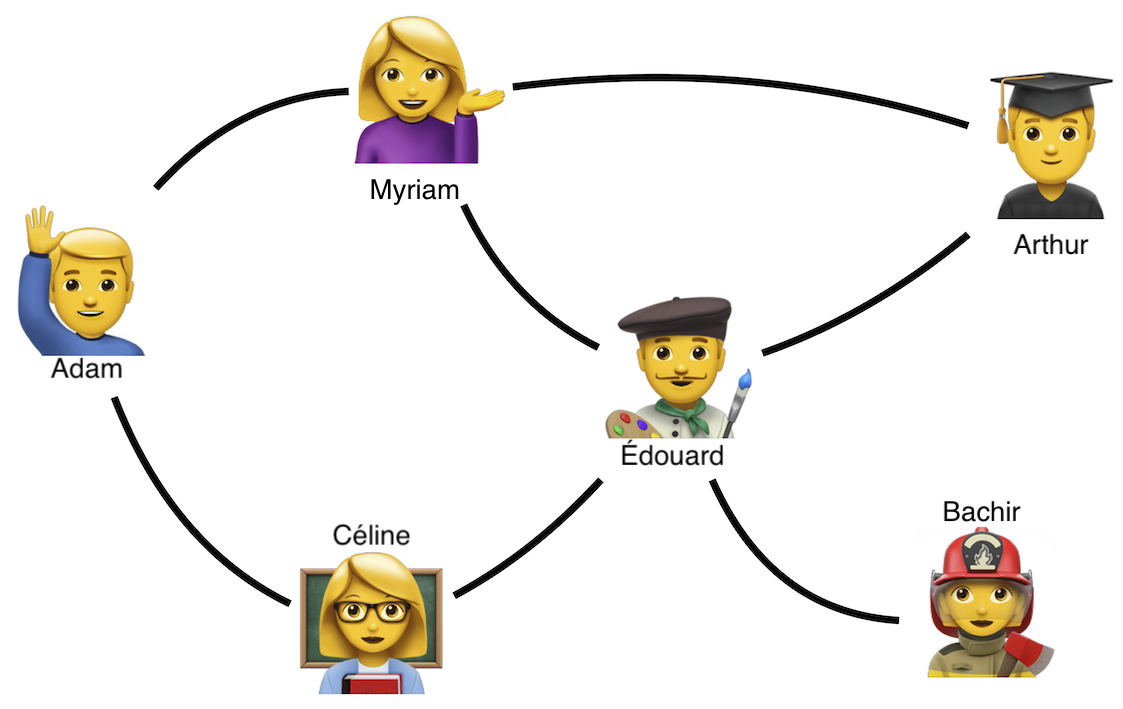
Question 4 Donner une liste d’adjacence du graphe ci-dessus. Notons que le graphe est non orienté : quelle propriété a la matrice d’adjacence, obtenue à l’aide des fonctions précédentes, dans ce cas ?

Question 5 C’est bien connu, “les amis de mes amis sont mes amis”. Comment obtenir la matrice d’adjacence du graphe des amis à distance 1 ou 2, c’est-à-dire le graphe reliant deux personnes si elles sont amies, ou si elles ont un ami commun. On pourra utiliser la fonction dot de la bibliothèque numpy pour réaliser un produit matriciel.

Plus généralement, on pourrait vouloir connaître toutes les personnes qui sont reliées à moi par un chemin d’amitié. Dans l’exemple précédent, tout le monde est alors relié à tout le monde, mais dans un graphe (possiblement orienté), ça n’est pas toujours le cas. La clôture transitive d’un graphe orienté \(G\) est le graphe obtenu en reliant un sommet \(u\) au sommet \(v\) s’il existe un chemin de \(u\) à \(v\) dans \(G\).

Question 6 Implémenter une fonction renvoyant la matrice d’adjacence de la clôture transitive d’un graphe donné en argument comme une matrice d’adjacence.

Les graphes des réseaux sociaux ont une propriété empiriquement vérifiée : la propriété de petit monde. Ainsi, “un utilisateur de Facebook (parmi les 1,59 milliards d’utilisateurs) est connecté à n’importe quelle autre personne par le biais de 3,5 personnes en moyenne.” (https://research.fb.com/three-and-a-half-degrees-of-separation/) Dit autrement, le diamètre d’un graphe de réseau social est toujours relativement petit, où le diamètre d’un graphe est la longueur maximale du plus court chemin séparant deux sommets.

Question 7 Modifier la fonction précédente pour obtenir le diamètre du graphe donné en argument.

Modélisation d’une énigme

Dans le film (), les deux héros, John McClane et Zeus Carver, doivent résoudre l’énigme de Simon Gruber pour arrêter le compte à rebours d’une bombe. Voici l’énigme: Sur la fontaine, il y a deux bidons: l’un a une contenance de 5 gallons, l’autre de 3 gallons. Remplissez l’un des bidons de 4 gallons d’eau exactement et placez-le sur la balance. La minuterie s’arrêtera. Soyez extrêmement précis: un gramme de plus ou de moins et c’est l’explosion! . Les nerfs de John McClane sont alors mis à rude épreuve pour trouver une solution. Il commence par remarquer très justement qu’on ne peut pas remplir le bidon de 3 gallons avec 4 gallons d’eau. Il faut donc trouver le moyen de mettre exactement 4 gallons d’eau dans le bidon de 5 gallons. Dans la scène du film (que vous pouvez consulter en français sur https://www.youtube.com/watch?v=pmk2mNf9iqE), John commence par donner une première idée peu convaincante puisqu’elle termine par la nécessité de remplir le bidon de 3 gallons au tiers, ce qu’on ne sait faire précisément… Le film propose ensuite une solution très partielle, coupée au montage. Appliquons donc des méthodes de graphes orientés pour retrouver la meilleure solution possible que les héros appliquent pour s’en sortir.

Une configuration du système correspond au volume d’eau contenu dans chacun des deux bidons. On peut donc représenter une telle configuration par une paire \((a,b)\) où \(a\) est le volume d’eau contenu dans le bidon de 5 gallons et \(b\) le volume d’eau contenu dans le bidon de 3 gallons, avec \(0\leq a \leq 5\) et \(0\leq b\leq 3\). Les actions élémentaires possibles du système sont de remplir un des deux bidons (qu’il soit initialement vide ou pas), vider un des deux bidons (qu’il soit initialement plein ou pas) et transférer le contenu d’un des bidons dans l’autre jusqu’à ce que ce dernier soit plein.

Question 8 En partant de la configuration initiale \((0,0)\), construire le graphe orienté décrivant entièrement l’ensemble des configurations et la dynamique du système.

Question 9 En déduire une solution la plus courte possible permettant d’aller de la configuration \((0,0)\) à une configuration de la forme \((4,b)\) où exactement 4 gallons d’eau se trouvent dans le gros bidon. Décrire à John McClane la suite d’opérations qu’il doit effectuer pour arrêter la bombe au plus vite.

Question 10 Imaginons la suite de l’énigme désormais. Dans une autre fontaine, le terroriste a placé deux bidons, l’un de 6 gallons et l’autre de 15 gallons. S’il demande à John McClane de remplir l’un des deux bidons avec exactement 5 gallons d’eau, pourra-t-il éviter l’explosion de la bombe?

Degrés et circuits eulériens

On appelle degré d’un sommet \(u\), dans un graphe non orienté, le nombre de sommets \(v\) voisins de \(u\), c’est-à-dire tels que \(\{u,v\}\in A\). On appelle degré sortant (respectivement entrant) d’un sommet \(u\), dans un graphe orienté, le nombre de sommets \(v\) tels que \((u,v)\in A\) (respectivement \((v,u)\in A\)).

Question 11 Écrire une fonction permettant de calculer un dictionnaire associant à chaque sommet du graphe son degré sortant (ou son degré) en fonction du dictionnaire représentant la liste de successeurs du graphe.

Une propriété intéressante des graphes non orientés concerne l’existence de cycles eulériens, c’est-à-dire de cycle (un chemin qui arrive là où il a commencé) empruntant une et une seule fois chacune des arêtes du graphe. Le problème prend le nom du mathématicien Euler qui a mis au jour ce problème dans le cadre d’une visite de la ville de Königsberg dont les rives sont reliées par 7 ponts :


On peut représenter une telle ville par un graphe non orienté avec un sommet par rive et une arête par pont :

 

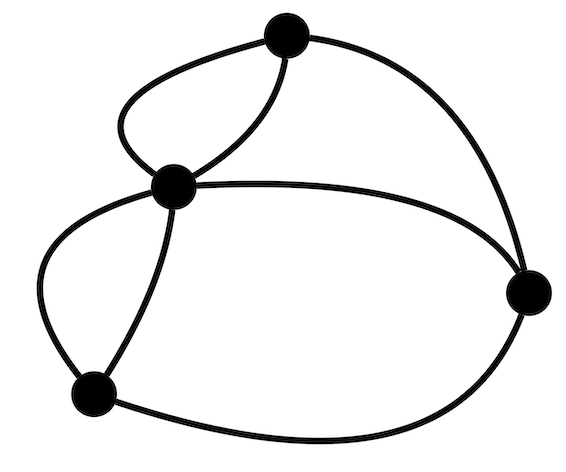
Le problème d’Euler est de trouver un itinéraire touristique visitant la ville de Königsberg en empruntant chaque pont une et une seule fois, c’est-à-dire de trouver un cycle eulérien dans le graphe de la ville. Après avoir un peu cherché, on se rend vite compte que cela n’est pas possible à Königsberg. Euler a réussi à caractériser les graphes possédant un cycle eulérien (on parle de graphe eulérien dans ce cas): un graphe non orienté possède un cycle eulérien si et seulement si tous ses sommets sont de degré pair. Vous pouvez aller voir sur internet ou dans de nombreux livres une preuve de ce théorème…

Question 12 En déduire une fonction testant si un graphe est eulérien.

Question 13 Une chaîne est dite eulérienne si elle emprunte une et une seule fois chaque sommet. Certains graphes ne possèdent pas de cycle eulérien, mais possèdent une chaîne eulérienne. Trouverez-vous comment adapter la condition nécessaire et suffisante d’Euler pour caractériser les graphes possédant une chaîne eulérienne ? Commencez par étudier des exemples de graphes…