-
Cours :
- Codage des nombres
- cours 1
transparents : pdf, html - planche de TD/TP 1 (pdf)
- cours 1
- Texte, fichiers et images
- cours 2
transparents : pdf, html - planche de TD/TP 2 (pdf)
- cours 2
- Tests
- cours 3
transparents : pdf, html - planche de TD/TP 3 (pdf)
- cours 3
- HTML/CSS
- cours 4
transparents : pdf, html - planche de TD/TP 4 (pdf)
- cours 4
- Javascript 1.0
- cours 5
transparents : pdf, html - planche de TD/TP 5 (pdf)
- cours 5
- Javascript 2.0
- Diviser pour régner
- cours 7
transparents : pdf, html - planche de TD/TP 7 (pdf)
- cours 7
- Didactique
- cours 8
transparents : pdf, html - planche de TD/TP 8 (pdf)
- cours 8
Codage des nombres
Représentation des entiers naturels (rappel)
Système de numération
Système conventionnel de comptage en base 10 incompatible avec la machine \(\Longrightarrow\) Étude d’autres systèmes de numération
Systèmes de numération : utilisation de symboles appelés chiffres (digits en anglais)
Le nombre de chiffres utilisés correspond à la base du système :
- Système binaire : base 2 (symboles ou chiffres : 0 et 1)
- Système décimal : base 10 (symboles ou chiffres : 0 à 9)
- Système Hexadécimal : Base 16 (symboles ou chiffres : 0 à 9, et A B C D E F)
Entier naturel en base \(\beta\)
Formule pour la valeur d’un nombre entier représenté en base \(\beta\)
\[c_nc_{n-1}\dots c_1c_0|_\beta= \sum_{i=n}^{i=0} (c_i\beta^i) = c_n\beta^n+ \cdots +c_2\beta^2+c_1\beta^1+c_0\beta^0\]
où \(c_i\) est le chiffre de rang \(i\) : le rang 0 correspond au chiffre le plus à droite.
Système binaire
- 2 chiffres : 0 et 1 (Vrai et Faux, ON et OFF, Oui et Non)
- On adapte la formule magique :
\[c_nc_{n-1}\dots c_1c_0|_2 = \sum_{i=n}^{i=0} (c_i2^i) = c_n2^n+ \cdots +c_22^2+c_12+c_0\]
Exemple
\[ \begin{array}{lll} 2019|_{10} & = & 1\times 1024+1\times 512+1\times 256+1\times 128+1\times 64 \\ & & + 1 \times 32+0\times 16+0\times 8+ 0\times 4+1\times 2+1\times 1\\ & = & 11111100011|_2 \end{array} \]
Le Système hexadécimal
- puissance de 2 et donc facile à convertir vers et depuis la base 2
- Plus lisible que le binaire : par exemple 10101001011010101010 et 10101011010101010011 en binaire versus A96AA et AB553 en hexadécimal
- 16 chiffres : 0, 1, 2, …, 9, A, B, C, D, E, F
- On adapte la formule magique :
\[c_nc_{n-1}\dots c_1c_0|_{16} = \sum_{i=n}^{i=0} (b_i16^i) = b_n16^n+ \cdots +b_216^2+b_116+b_0\]
Exemple
\[ 2019|_{10} = 7 \times 16^2 + 14 \times 16 + 0 = 7 \times 16^2 + E \times 16 + 0 = 7F3|_{16} \]
Nombre de chiffres pour représenter un nombre
Définition
On note \(n+1=N_{\beta}(x)\) le nombre de chiffres nécessaires pour exprimer \(x\) dans la base \(\beta\).
Théorème
\(N_{\beta}(x)\) est le plus petit entier strictement supérieur à \(\log_\beta(x)\)
Corollaire
Le rapport \(\frac{N_\beta(x)}{N_{\beta'}(x)}\) tend vers \(\frac{\ln(\beta')}{\ln(\beta)}\) quand \(x\) tend vers l’infini
Exemple
Pour écrire un grand nombre en base \(2\), il faut environ \(3,32\) fois plus de chiffres qu’en base \(10\) car \(\frac{\ln(10)}{\ln(2)} = 3,32\dots\)
Représentation des entiers relatifs
Représentation avec bit de signe
- un bit pour représenter le signe (positif ou négatif) et codage binaire de la valeur absolue
- Deux zéros : un positif et un négatif
- Sur un octet (8 bits), on représente les entiers de \(-2^{7}+1=-127\) à \(2^7 -1 = 127\)
- Sur deux octets (16 bits), on représente les entiers de \(-2^{15}+1=-32767\) à \(2^{15} -1=32767\)
Alternative : le complément à deux
Toujours un bit pour coder le signe, mais une autre façon de coder la valeur absolue
Méthode pour obtenir la représentation
- On exprime la valeur absolue en base \(2\)
- Ensuite on complémente à deux si on code une valeur négative :
- On inverse tous les bits (\(1\rightarrow 0\) et \(0\rightarrow 1\))
- Ajoute 1 au résultat en ignorant le bit supplémentaire si on dépasse le nombre de bits fixé
Remarques
- Une seule façon de coder 0 : 00000000 00000000
- Un négatif de plus !
Exemples complément à deux sur 2 octets
\[ \begin{array}{ccl} 1 & = & (0000000000000001) \\ -1 & = & (1111111111111111) \\ 3 & = & (0000000000000011) \\ -3 & = & (1111111111111101) \\ 32767 & = & (0111111111111111) \\ -32767 & = & (1000000000000001) \\ -32768 & = & (1000000000000000) \\ \end{array} \]
Répartition des entiers dans le complément à deux
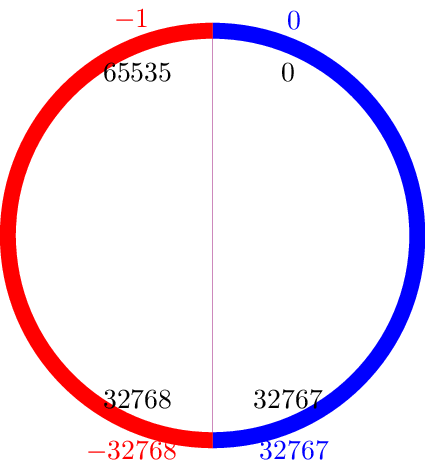
Pourquoi utiliser cette représentation?
Pour que l’addition entre deux nombres soit correcte quelque soit leur signe.
\[ \begin{array}{rr} ~0000000000000011& 3\\ \underline{+1111111111111111}& \underline{+(-1)} \\ 1 0000000000000010 & 2 \end{array} \]
Opérations en binaire
Addition en binaire
On additionne les chiffres un par un en partant de la droite comme pour la base 10.
On additionne les deux chiffres plus la retenue :
- Si le résultat est 0 : on écrit 0 et on retient 0
- Si le résultat est 1 : on écrit 1 et on retient 0
- Si le résultat est 2 : on écrit 0 et on retient 1
- Si le résultat est 3 : on écrit 1 et on retient 1
Exemple addition en binaire
\[ \begin{array}{rrrrrrrrrr} {~^1}&{~^1}&{~^1}&{~^1}&&{~^1}&&&&\\ ~&1&1&0&1&0&1&1&0&0\\ +&1&0&1&1&0&1&0&1&0\\ \hline 1&1&0&0&0&1&0&1&1&0 \end{array} \]
Soustraction en binaire
On soustrait les chiffres un par un en partant de la droite.
On soustrait au chiffre en haut le chiffre en bas plus la retenue :
- Si le résultat est 1 : on écrit 1 et on retient 0
- Si le résultat est 0 : on écrit 0 et on retient 0
- Si le résultat est -1 : on écrit 1 et on retient -1
- Si le résultat est -2 : on écrit 0 et on retient -1
Exemple soustraction en binaire
\[ \begin{array}{rrrrrrrrrr} &{~^{-1}}&{~^{-1}}&{~^{-1}}&{~^{-1}}&&{~^{-1}}&&&\\ ~&1&1&0&0&0&1&0&0&1\\ -&0&1&1&0&1&0&1&0&0\\ \hline &~0&~1&~0&~1&~1&~0&~1&~0&~1 \end{array} \]
Multiplication en binaire
On multiplie le premier nombre par chacun des chiffres du deuxième :
- si le chiffre est 1 on recopie le premier nombre suivi d’un nombre de 0 égal au rang du chiffre.
- si le chiffre est 0 : on ne fait rien.
On additionne les nombres ainsi obtenus pour avoir le résultat final.
Exemple multiplication en binaire
\[ \begin{array}{r} 110001001\\ \times 10101\\ \hline 110001001\\ +11000100100\\ +1100010010000\\ \hline 10000000111101 \end{array} \]
Représentation des réels
Représentation des nombres réels
Représentation en base deux d’un réel
Les chiffres après la virgule ont des rangs négatifs et sont donc multipliés par des puissances de 2 négatives :
\[c_nc_{n-1}\dots c_1c_0,c_{-1}c_{-2}c_{-3}\dots|_2= \sum_{i=-\infty}^{i=n} (c_i2^i)\]
Problématiques de la représentation des réels en machines
- assurer la précision derrière la virgule
- pouvoir représenter de grands nombres
Solutions classiques
- Virgule fixe
- Virgule flottante
Virgule fixe
Nombre fixe de chiffres après la virgule
- Opérations plus simples \(\rightarrow\) processeurs moins chers
- Plus facile à coder dans la machine
Deux parties
- La partie entière codée en binaire (complément à deux)
- La partie décimale : chaque bit correspond à l’inverse d’une puissance de \(2\)
Exemple
\[ \begin{array}{rcc} -3,625_{10} = & \underbrace{1111111111111101}&\underbrace{1010000000000000}\\ & -3 & 0,625 = 0,5+0,125 = \frac{1}{2}+\frac{0}{4}+\frac{1}{8} \end{array} \]
Limites de la représentation en virgule fixe
Représentation rigide
- Petits nombres : gaspillage des chiffres à gauche de la virgule
- Peu de décimales : gaspillage à droite
- Plus simple à mettre en œuvre, pour des ordres de grandeur comparables
Bornes
Si \(n\) est le nombre de bits de la partie entière, et \(d\) est le nombre de bits de la partie fractionnaire
- Borne maximale : \(2^ {n-1}-\frac{1}{2^d}\)
- Borne minimale : \(-2^{n-1}\)
Virgule flottante
Solution la plus répandue
- Norme IEEE 754: deux formats (32 bits et 64 bits) selon précision (simple et double)
- Utilisés dans tous les ordinateurs actuels : implémentation matérielle de ce codage par le processeur.
Un triplet pour coder une valeur
- Le signe \(s\) (sur un bit)
- La mantisse \(m\)
- L’exposant \(e\) : \(x = sm\beta^e\)
Exemples
\[-1540,412654 = -1,540412654. 10^3\] \[101110,001101 = 1,01110001101\times 2^5\]
Virgule flottante IEEE 754
- Mantisse de taille fixée
- On fait flotter la virgule en faisant varier \(e\) pour que le premier chiffre significatif (\(\neq 0\)) soit juste avant la virgule
- En base 2, le chiffre significatif est égal à 1 et il suffit donc de coder les chiffres après la virgules.
- Deux précisions possibles :
| mantisse | exposant | taille totale | |
|---|---|---|---|
| Simple précision | 23 | 8 | 32 |
| Double précision | 52 | 11 | 64 |
Exemple de représentation d’un nombre
\(-6,625_{10}\) En simple précision
- Binaire (valeur absolue) : 110,101
- Normalisation de la mantisse : \(1,10101. 2^2\)
- Occupation des \(24\) bits de mantisse \(1,\underbrace{10101000000000000000000}\)
- Décalage de l’exposant (en simple précision \(127\)) donc exposant = \((2+127)_{10} = 10000001_2\)
- Signe = \(1\) car négatif
On obtient donc :
\[ \begin{array}{ccc} \underbrace{1} & \underbrace{10000001}&\underbrace{10101000000000000000000}\\ \mathrm{signe} & \mathrm{exposant} & \mathrm{mantisse} \end{array} \]
Bugs dus à la représentation des nombres
Patriot Missile Failure (virgule fixe)
- Anti missile Patriot : mesure du temps par une horloge cadencée au dixième de seconde, dès leur mise sous tension.
- Durée écoulée = nb de tics x \(\frac{1}{10}\).
- Le nombre \(\frac{1}{10}\) est codé en virgule fixe sur 24 bits :
\(0.1 = 0.00011001100110011001100\) - L’erreur commise sur la fraction est donc :
\(0.000000000000000000000001100 \approx 9.54 \times 10^{-8}\) - 100 h après le boot : décalage d’horloge de : \(100 \times 3600 \times 10 \times 9.54 \times 10^{-8} = 0,34\,s\)
- Vitesse de 1 676 m/s \(\Rightarrow\) \(0,34\times 1676 > 500\, m\) (hors fenêtre)
Cet incident qui a coûté la vie à plusieurs dizaines de personnes le 25 février 1991. Source : Rapport du Gao
Ariane V (conversion)
Le 4 Juin 1996, le vol 501 (Ariane 5) explose 37 secondes après le décollage.
Le problème vient d’une erreur logicielle.
Un nombre flottant (accélération horizontale), codé sur 64 bits est converti en entier signé. Sa valeur dépasse le plus grand entier signé représentable sur 16 bits et la conversion échoue (exception) provoquant une erreur dans le système de référence inertielle. Source : Flight 501 Failure
Bourse de Vancouver (arrondis)
En 1984, la bourse de Vancouver crée son indice (qui indique si la bourse est en hausse ou en baisse) initialisé à 1000. Il est recalculé 3000 fois par jour. À chaque fois, on ne conserve que 3 décimales (troncature).
\(\Rightarrow\) Au bout de 10 ans, l’indice vaut 500
Sa valeur réelle est pourtant > à 1000.
Source : The Wall Street Journal November 8, 1983, p. 37
Bug des GPS
Le compteur des semaines d’un GPS grand public est un entier codé sur 10 bits. Après la semaine 1023, on passe à la semaine 0… Ceci (Week Number Roll0ver ou WNRO) s’est produit pour la première fois le 21 août 1999 et se reproduira le 6 avril 2019.
Source : Memorandum on GPS