Cours Génie logiciel

Planches de TD :
- TD 1 (pdf), Corrigé TD 1 (pdf)
- TD 2 (pdf), Corrigé TD 2 (pdf)
Planches de TP :
- TP 1 (pdf), Corrigé TP 1 (pdf)
- TP 2 (pdf), Corrigé TP 2 (pdf)
- TP 3 (pdf)
- TP 4 (pdf), Corrigé TP 4 (pdf)
- TP 5 (pdf)
- TP 6 (pdf)
Polycopiés de cours :
- Introduction (pdf)
- Gestion de versions (pdf)
- Tests (pdf)
- Documentation (pdf)
- UML (pdf)
- Principes SOLID (pdf)
- Patrons de conception (pdf)
Annales :
- Sujet blanc, Corrigé
- Examen 2024-2025 (session 1), Corrigé

Formules

Introduction

Le but de ce projet est d’implémenter des classes pour générer des formules mathématiques. Chaque classe correspondra à un type de formule (constantes, variable, addition, multiplication, …). Le but de ce TP est de travailler les patrons de conception suivants :

Composite
Template method
Strategy
Abstract factory
Visitor

Création de projet

Pour la création du dépôt, il vous faut suivre les consignes du TP précédent.

Consignes pour le rendu

Rendu via `etulab`

Le rendu de votre projet formula est à faire pour le 5 novembre 2024. Il faudra que le dépôt git sur etulab soit à jour pour le 5 novembre 2024 à 23h59 et que l’enseignant suivant soit membre du projet avec des droits au moins égal à reporter : Arnaud Labourel, identifiant alaboure.

L’ajout de membre se fait via manage $\rightarrow$ members dans le menu de votre projet sur etulab, puis en cliquant sur le bouton invite members.

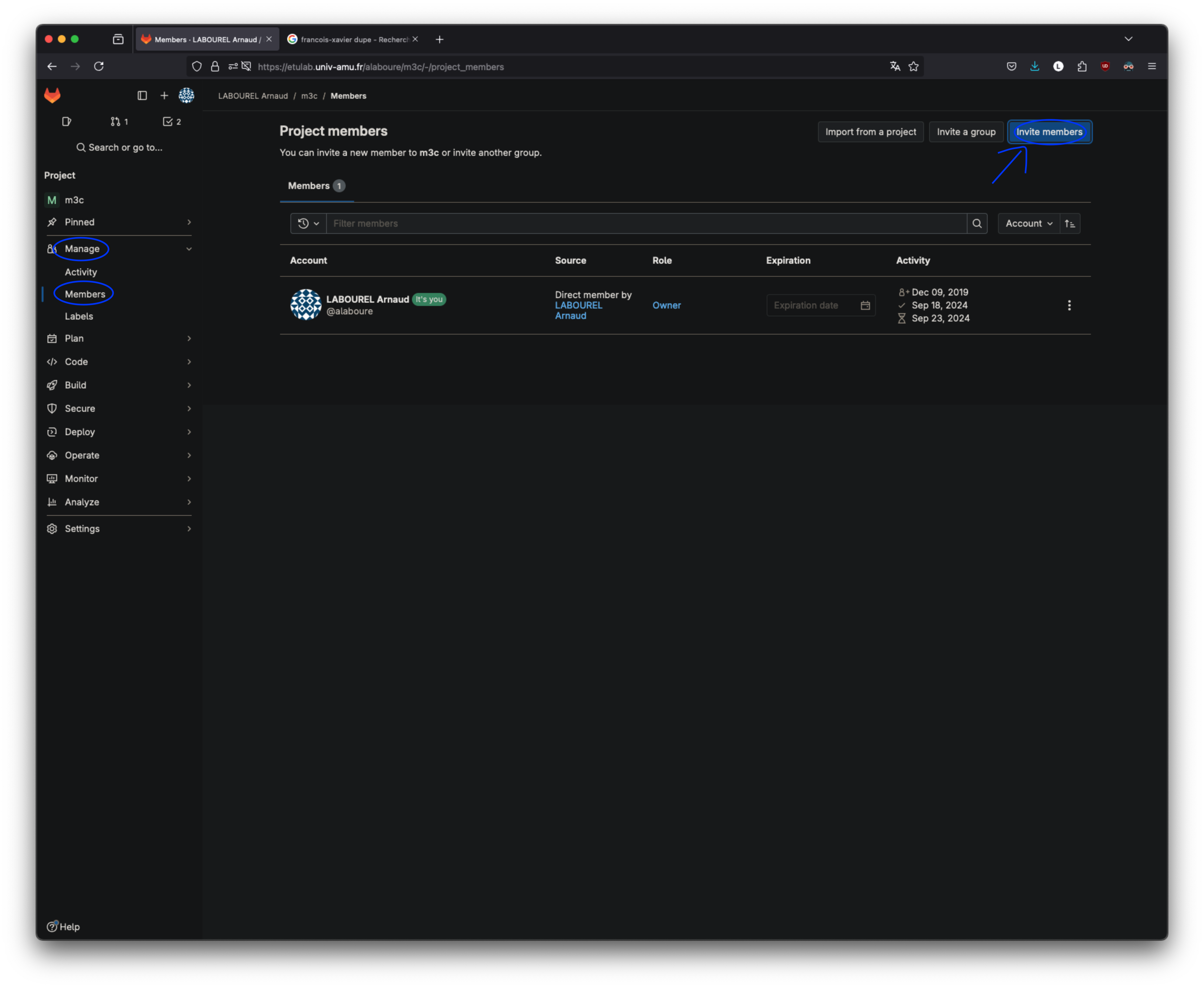
Le travail peut être réalisé seul ou en binôme. Dans le cas de binôme, les deux étudiants devront être membres du projet.

Respect de la propriété intellectuelle

Comme pour tout devoir, nous vous demandons de ne pas partager votre programme, complet ou partiel, avec des étudiants n’étant pas membres de votre projet. Tout emprunt que vous effectuez doit être proprement documenté en indiquant quelle partie de votre programme est concernée et de quelle source elle provient (nom d’un autre étudiant, site internet, …). Les emprunts incluent l’utilisation d’IA génératives telles que ChatGPT qui devront donc aussi être documentés.

Fichier `README.md` du projet

Votre projet devra contenir à sa racine un fichier README.md contenant les informations sur ces membres et les emprunts réalisés. Le format du fichier devra être le suivant :

# Formule

## Membres du projet

- NOM Prénom du premier membre 
- NOM Prénom du deuxième membre (si applicable)

## Description des emprunts

- Utilisation de ChatGPT pour les classes : `Main.java`, ...
- ...

Critères d’évaluation

Vous serez évalué sur :

La conception logicielle : votre projet devra dans la mesure du possible respecter les bonnes pratiques de conception logicielle en programmation orientée objet tels que les principes SOLID. Par exemple, des classes ayant trop de responsabilités vous pénaliseront.
La propreté du code : comme indiqué dans le cours, il est important de programmer proprement. Des répétitions de code trop visibles, des noms mal choisis ou des fonctions ayant beaucoup de lignes de code (plus de dix) vous pénaliseront. Le sujet vous donne les méthodes que vous devez absolument écrire, mais il est tout à fait autoriser d’écrire des méthodes supplémentaires, de créer des constantes, … pour augmenter la lisibilité du code. On rappelle que vous devez écrire le code en anglais.
La correction du code : on s’attend à ce que votre code soit correct, c’est-à-dire qu’il respecte les spécifications dans le sujet. Comme indiqué dans le sujet, vous devez tester votre code pour vérifier son comportement.
Les commit/push effectués : il vous faudra travailler en continu avec git et faire des push/commit le plus régulièrement possible. Un projet ayant très peu de pushs/commits effectués juste avant la date limite sera considéré comme suspicieux et noté en conséquence. Un minimum accepté pour le projet sera d’au moins 2 pushs sur deux jours différents et d’au moins 10 commits au total. Dans le cas d’un projet réalisé en binôme, chacun des deux membres du projet devra réaliser au moins un push.

Tâches à réaliser

Interface `Formula`

La première chose à faire est de définir une interface correspondant à une formule. Une formule aura deux méthodes, une méthode asString() renvoyant une chaîne de caractères représentant la formule et une méthode asValue() renvoyant la valeur de la formule sous forme d’un double. L’interface devra donc correspondre au diagramme de classe suivant :

Tâche 1 : Créez l’interface Formula dans le répertoire src/main/java de votre projet.

Classe `Constant`

La classe Constant permet de représenter une formule correspondant à une constante.

Tâche 2 : Créez la classe Constant dans le répertoire src/main/java de votre projet.

Tâche 3 : Créez une classe de test nommée ConstantTest dans le répertoire src/test/java de votre projet qui devra vérifier via des tests unitaires le comportement de la classe Constant. Vous devez tester les comportements suivants :

new Constant(3.1).asValue() retourne une valeur égale à 3.1 ;
new Constant(3.1).asString() retourne une chaîne de caractères égale à "3.1" ;

Classe `Variable`

La classe Variable permet de représenter une formule correspondant à une variable.

Tâche 4 : Créez la classe Variable dans le répertoire src/main/java de votre projet.

Tâche 5 : Créez une classe de test nommée VariableTest dans le répertoire src/test/java de votre projet qui devra vérifier via des tests unitaires le comportement de la classe Variable. Vous devez tester les comportements suivants :

new Variable("X", 3.1).asValue() retourne une valeur égale à 3.1 ;
new Variable("X", 3.1).asString() retourne une chaîne de caractères égale à "X" ;

Classe `Sum`

La classe Sum permet de représenter une formule correspondant à une somme d’au moins deux autres formules.

Tâche 6 : Créez la classe Sum dans le répertoire src/main/java de votre projet.

Tâche 7 : Créez une classe de test nommée SumTest dans le répertoire src/test/java de votre projet qui devra vérifier via des tests unitaires le comportement de la classe Sum. Vous devez tester les comportements suivants :

new Sum(new Variable("Y", 4.3), new Variable("X", 3.1)).asValue() retourne une valeur proche de 7.4 ;
new Sum(new Variable("Y", 4.3), new Variable("X", 3.1), new Variable("Z", 1.1)).asValue() retourne une valeur proche de 8.5 ;
new Sum(new Variable("Y", 4.3), new Variable("X", 3.1)).asString() retourne une chaîne de caractères égale à "(Y + X)" ;
new Sum(new Variable("Y", 4.3), new Variable("X", 3.1), new Variable("Z", 1.1)).asString() retourne une chaîne de caractères égale à "(Y + X + Z)"

Classe `Product`

La classe Product permet de représenter une formule correspondant à un produit d’au moins deux autres formules.

Tâche 8 : Créez la classe Product dans le répertoire src/main/java de votre projet.

Tâche 9 : Créez une classe de test nommée ProductTest dans le répertoire src/test/java de votre projet qui devra vérifier via des tests unitaires le comportement de la classe Product. Vous devez tester les comportements suivants :

new Product(new Variable("Y", 4.3), new Variable("X", 3.1)).asValue() retourne une valeur proche de 13.33 ;
new Product(new Variable("Y", 4.3), new Variable("X", 3.1), new Variable("Z", 1.1)).asValue() retourne une valeur proche de 14.663 ;
new Product(new Variable("Y", 4.3), new Variable("X", 3.1)).asString() retourne une chaîne de caractères égale à "(Y * X)" ;
new Product(new Variable("Y", 4.3), new Variable("X", 3.1), new Variable("Z", 1.1)).asString() retourne une chaîne de caractères égale à "(Y * X * Z)"

Réécriture code classes `Sum` et `Product`

On peut remarquer que les codes des classes Sum et Product sont très similaires.

En effet, les attributs et le code des constructeurs sont identiques. De plus, il est possible de rendre identique les codes des méthodes String asString() et double asValue() en effectuant quelques modifications.

Dans la méthode String asString(), seul le caractère inséré entre les formules est différent. Dans chacune des classes Sum et Product, il est possible de définir une méthode String symbol() qui retourne ce caractère puis de réécrire les méthodes String asString() de Sum et Product de sorte qu’elles utilisent la méthode String symbol().
De même, on peut faire que le code de la méthode asValue() soit le même dans les classes Sum et Product. Pour cela, on peut définir les méthodes double initialValue() et double cumulativeValue(double accumulator, double value) dans les classes Sum et Product qui retournent les valeurs suivantes :

Méthodes\Classes Sum Product

initialValue 0 1

cumulativeValue accumulator+value accumulator*value

On peut ensuite réécrire la méthode asValue() des classes Sum et Product de sorte qu’elles utilisent les méthodes initialValue et cumulativeValue.

Méthodes\Classes	`Sum`	`Product`
`initialValue`	0	1
`cumulativeValue`	accumulator+value	accumulator*value

Réécriture par extension

On va commencer par appliquer le patron de conception template method (patron de méthode). On va donc créer une classe abstraite VariadicOperator contenant le code en commun entre Sum et Product. La classe VariadicOperator aura trois méthodes abstraites : intialValue, cumulativeValue et symbol. Les nouvelles classes Sum et Product étendront la classe VariadicOperator en implémentant ces trois méthodes abstraites. On aura donc la configuration suivante :

Tâche 10 : Créez un package extension dans le répertoire src/main/java de votre projet.

Tâche 11 : Remplacez les anciennes classes Sum et Product par les nouvelles classes Sum et Product que vous mettrez dans le package extension de votre projet. Vérifiez que les tests des classes passent toujours.

Réécriture par délégation

Pour cette autre façon de factoriser le code entre les classes Sum et Product, on va créer une nouvelle classe VariadicOperator dans un nouveau package strategy. Cette nouvelle classe délèguera les parties spécifiques de l’évaluation et de représentation en chaîne de caractères à une interface Operator. L’interface Operator contiendra les trois méthodes symbol, initialValue et cumulativeValue et sera implémenté par deux classes Addition et Multiplication. On aura donc le diagramme de classes suivant :

Tâche 12 : Créez un package strategy dans le répertoire src/main/java de votre projet.

Tâche 13 : Créez les classes Addition, Multiplication et l’interface Operator dans le package strategy de votre projet.

Tâche 14 : Créer une nouvelle classe VariadicOperator dans le package extension (sans supprimer la classe VariadicOperator du package extension) de votre projet.

Tâche 15 : Créer des classes VariadicOperatorTest, AdditionTest et MutiplicationTest dans le répertoire src/test/java de votre projet qui devront vérifier via des tests unitaires le comportement des classes VariadicOperator, Addition et Mutiplication.

Parseur formule notation postfixée

Nous souhaitons écrire un programme qui prend en paramètre une expression en notation postfixée composée de nombres (constantes), de + et de * et qui calcule la valeur de l’expression. En notation postfixée (ou polonaise inversée), on place l’opérateur à droite des deux opérandes (on supposera que les opérations + et * sont binaires et ne s’appliquent donc que sur les deux derniers termes). Par exemple, l’expression (2 * 5) + 3 * (4 + 7) s’écrit en notation postfixée 2 5 * 3 4 7 + * + (les parenthèses sont inutiles).

Le but est donc de créer une classe FormulaParser qui va créer une formule (interface Formula) à partir d’une chaîne de caractère. Cette classe FormulaParser correspondra au diagramme suivant :

Les méthodes de FormulaParser ont le comportement suivant :

Formula analyze(String... tokens) analyse les tokens d’une expression postfixée et retourne une formule correspondant à l’expression. Par exemple, un appel à analyze("2", "5", "*", "3", "4", "7", "+", "*", "+") devra renvoyer une formule équivalente à la formule add2 obtenu par le code suivant :
```
Formula mult1 = new Product(new Constant(2), new Constant(5));
Formula add1 = new Sum(new Constant(4), new Constant(7));
Formula mult2 = new Product(new Constant(3), add);
Formula add2 = new Sum(mult1, mult2);
```
Le code de la méthode analyze créera une pile vide de formules et parcourra les tokens et appellera analyzeToken sur chacun des tokens. Finalement, le retour de la méthode sera obtenu en dépilant la pile.
void analyzeToken(String token, Stack<Formula> stack) traite une token en appelant une des méthodes analyzeSum, analyzeProduct ou analyzeDouble en fonction du type de token : "+", "*" ou un double.
void analyzeSum(Stack<Formula> stack) dépile deux éléments de la pile (levant une exception de type IllegalStateException si la pile ne contient pas assez d’éléments) afin de créer une Sum avec ces deux formules puis de l’empiler.
void analyzeProduct(Stack<Formula> stack) dépile deux éléments de la pile (levant une exception de type IllegalStateException si la pile ne contient pas assez d’éléments) afin de créer un Product avec ces deux formules puis de l’empiler.
void analyzeDouble(String doubleToken, Stack<Formula> stack) empile une constante ayant la valeur du token.

Tâche 16 : Créer une nouvelle classe FormulaParser dans le répertoire src/main/java de votre projet.

Tâche 17 : Créer la classe FormulaParserTest dans le répertoire src/test/java de votre projet qui devront vérifier via des tests unitaires le comportement de la classe FormulaParser. Pour tester certains comportements, vous aurez besoin de redéfinir la méthode equals (déjà défini dans Object) dans les classes Sum, Product et Constant afin de considérer égales les sommes (ou les produits) sommant des formules égales et les constantes de valeur égale.

Réécriture avec une fabrique abstraite

Si on souhaite utiliser la classe VariadicOperator du package strategy à la place des classes Sum et Product du package extension, on doit modifier à plusieurs endroits le code de FormulaParser. Ce n’est pas satisfaisant et on va donc créer une fabrique abstraite et changer le code de FormulaParser pour utiliser la fabrique abstraite pour construire les formules. Le diagramme de classes sera le suivant :

Tâche 18 : Créez l’interface FormulaFactory et les deux classes StrategyFormulaFactory et ExtensionFormulaFactory qui l’implémentent dans le répertoire src/main/java de votre projet

Tâche 19 : Modifiez le code de la classe FormulaParser pour qu’elle utilise une FormulaFactory pour créer les formules.

Utilisation du patron visitor

On souhaite utiliser le patron de conception visitor pour les classes implémentant Formula. Afin d’illustrer le comportement de ces trois visiteurs on considérera la formule formula construite grâce au code suivant :

Variable a = new Variable("a", 0.1);
Variable b = new Variable("b", 0.1);
Constant c = new Constant(0.1);
Variable d = new Variable("d", 1);
Formula formula = new Product(new Sum(new Sum(a,b), c), d);

On souhaite définir 3 types de visiteurs :

LatexVisitor : produit un texte LaTeX représentant la formule. Le symbole de l’addition est le + alors que la multiplication a pour symbole \times et la formule est entourée de $. La formule formula devra avoir la représentation LaTeX suivante : $(((a + b) + 0.1) \times d)$ .

XMLVisitor : produit un texte XML représentant la formule. On utilisera des balises <product>, <sum>, <variable> et <constant> correspondant aux différents types de formules. Pour les variables, on utilisera des balises <name> et <value> pour les attributs. La formule formula devra avoir la représentation XML suivante :

<product>
  <sum>
    <sum>
      <variable>
        <name>a</name>
        <value>0.1</value>
      </variable>
      <variable>
        <name>b</name>
        <value>0.1</value>
      </variable>
    </sum>
    <constant>0.1</constant>
  </sum>
  <variable>
    <name>d</name>
    <value>1.0</value>
  </variable>
</product>

PreciseEvaluatorVisitor : évalue la valeur de la formule en utilisant BigDecimal. Les calculs avec les doubles contiennent des imprécisions et par exemple la formule formula ne s’évalue pas à 0.3 lorsqu’on évalue avec les doubles. Une solution pour améliorer la précision des calculs est d’utiliser BigDecimal pour les opérations. L’objectif est d’obtenir une évaluation à 0.3 pour formula. Pour cela, il vous faudra créer les BigDecimal à partir des chaînes de caractères des valeurs des constantes et des variables (en utilisant le constructeur de BigDecimal prenant un String en argument) et utiliser les méthodes add et multiply de BigDecimal pour Sum et Product.

Le diagramme de classe sera le suivant :

Tâche 20 : Créez l’interface FormulaVisitor<R>.

Tâche 21 : Créez l’interface VisitableFormula qui étends l’interface Formula et définit une méthode <R> R accept(FormulaVisitor<R> visitor).

Tâche 22 : Modifiez les classes Variable et Constant pour qu’elles implémentent VisitableFormula au lieu de Formula et qu’elles définissent une méthode accept.

Tâche 23 : Modifiez les classes VariadicOperator, Sum et Product du package extension pour que VariadicOperator implémente VisitableFormula et que les classes Sum et Product définissent une méthode accept. Ajouter aussi des méthodes VisitableFormula[] getFormulas() dans Sum et Product afin que les visiteurs puissent avoir l’accès aux données des classes.

Tâche 24 : Créez la classe XMLVisitor implémentant FormulaVisitor<String> dans le répertoire src/main/java de votre projet.

Tâche 25 : Créez une classe de test nommée XMLVisitorTest dans le répertoire src/test/java de votre projet qui devra vérifier via des tests unitaires le comportement de la classe XMLVisitor.

Tâche 26 : Créez la classe PreciseEvaluatorVisitor implémentant FormulaVisitor<BigDecimal> dans le répertoire src/main/java de votre projet.

Tâche 27 : Créez une classe de test nommée PreciseEvaluatorVisitorTest dans le répertoire src/test/java de votre projet qui devra vérifier via des tests unitaires le comportement de la classe PreciseEvaluatorVisitor.

Tâche 28 : Créez la classe LatexVisitor implémentant FormulaVisitor<String>dans le répertoire src/main/java de votre projet.

Tâche 29 : Créez une classe de test nommée LatexVisitorTest dans le répertoire src/test/java de votre projet qui devra vérifier via des tests unitaires le comportement de la classe LatexVisitor.

Tâches supplémentaires

Les tâches décrites ci-dessous (tâches 30 et 31) peuvent être réalisée dans l’ordre de votre choix.

Visiteurs supplémentaires

Pour les fonctionnalités suivantes, on supposera que les formules sont uniquement composé de Variables, Constantes, Sommes et Produits. On souhaiterait avoir les classes suivantes :

Une classe IsConstantVisitor implémentant FormulaVisitor<Boolean> qui retourne pour chaque formule si elle correspond à une constante ou pas. Une formule correspond à une constante si elle est de type Constant ou bien si elle correspond à un produit ou une somme uniquement composée de constantes.
Une classe IsZeroVisitor implémentant FormulaVisitor<Boolean> qui retourne pour chaque formule si elle est toujours égale à 0 ou pas. Une formule est égale à zéro si elle est constante et s’évalue à 0 ou bien si elle correspond à un produit contenant une formule à zéro.
Une classe SimplifyVisitor implémentant FormulaVisitor<Formula> qui retourne une formule plus simple qui est équivalente à la formule donnée en paramètre. On considère par exemple la formule formula correspondant à l’expression $((3+3)\times x) + (0\times y)$ et pouvant être obtenue par le code suivant :
```
Variable x = new Variable("x", 0.1);
Constant c1 = new Constant(3);
Constant c2 = new Constant(3);
Constant zero = new Constant(3);
Variable y = new Variable("y", 0.1);
Formula formula = new Sum(new Product(new Sum(c1,c2), x), new Product(zero, y));
```
Un appel à formula.accept(new SimplifyVisitor()) (appliquant le visiteur à la formule) devra retourner une formule équivalente à la formule simplifiedFormula correspondant à l’expression $6\times x$ et pouvant être obtenue par le code suivant :
```
Formula simplifiedFormula = new Product(new Constant(6), x);
```
Une classe DerivativeVisitor implémentant FormulaVisitor<Boolean>, ayant un attribut String variableName initialisé à la construction via un argument du constructeur de même nom et type, qui retourne une formule correspondant à la dérivée de la formule par rapport à la variable de nom variableName. On considère par exemple la formule formula correspondant à l’expression $(3\times x) + y$ et pouvant être obtenue par le code suivant :
```
Variable x = new Variable("x", 0.1);
Variable y = new Variable("y", 0.1);
Formula formula = new Sum(new Product(new Constant(3), x), y);
```
Un appel à formula.accept(DerivativeVisitor("x")) (appliquant le visiteur à la formule) devra retourner une formule équivalente à la formule derivativeFormula correspondant à l’expression $((3\times 1) + (0\times x)) + 0$ et pouvant être obtenue par le code suivant :
```
Variable x = new Variable("x", 0.1);
Formula subFormula1 = new Product(new Constant(3), new Constant(1));
Formula subFormula2 = new Product(new Constant(0), x);
Formula derivativeFormula = new Sum(new Sum(subFormula1, subFormula2), new Constant(0));
```
On pourra appeler le visiteur de simplification derivativeFormula.accept(new SimplifyVisitor()) pour obtenir une formule simplifiée simplifiedDerivativeFormula correspondant à l’expression $3$ et pouvant être obtenue par le code suivant :
```
Formula simplifiedDerivativeFormula = new Constant(3);
```

Tâche 30 : Créez les classes décrites ci-dessus. Vous devez :

Tester les classes que vous créez ;
Faire attention à minimiser la duplication de code ;
Faire attention à respecter les principes SOLID ;
Ajouter les classes dans les fabriques abstraites ;
Ajouter les classes aux différents visiteurs ;
Modifier FormulaParser pour ajouter les opérations correspondant aux nouveaux types de formules.

Autres implémentations de `Formula`

On souhaite compléter les formules avec :

une classe Maximum minimum $\max(f_1, f_2, \dots, f_k)$ pour des formules $f_1, f_2, \dots ,f_k$ :
- représentation texte max(f,g,h) pour trois formules f, g et h,
- représentation XML <maximum> f g h </maximum> pour trois formules f, g et h,
- représentation latex \max(f,g,h) pour trois formules f, g et h;
une classe Minimum minimum $\min(f_1, f_2, \dots, f_k)$ pour des formules $f_1, f_2, \dots ,f_k$ :
- représentation texte min(f,g,h) pour trois formules f, g et h,
- représentation XML <minimum> f g h </minimum> pour trois formules f, g et h,
- représentation latex \min(f,g,h) pour trois formules f, g et h;
une classe Fraction fraction $f/g$ pour deux formules $f$ et $g$ :
- représentation texte f/g,
- représentation XML
```
<fraction> 
  <numerator>f</numerator>
  <denominator>g</denominator>
</fraction>
```
- représentation latex \frac{f}{g} ;
une classe Minus négation $-f$ pour une formule $f$ :
- représentation texte -f,
- représentation XML <minus>f</minus>,
- représentation latex -f ;
une classe AbsoluteValue valeur absolue $|f|$ pour une formule $f$ :
- représentation texte |f|,
- représentation XML <absoluteValue>f</absoluteValue>,
- représentation latex \lvert f \rvert ;
une classe Square carré $f^2$ pour une formule $f$ :
- représentation texte f²,
- représentation XML <square>f</square>,
- représentation latex f^2 ;
une classe SquareRoot carré $\sqrt{f}$ pour une formule $f$
- représentation texte sqrt(f),
- représentation XML <squareRoot>f</squareRoot>,
- représentation latex \sqrt{f} ;
une classe Power : puissance $f^g$ pour deux formules $f$ et $g$
- représentation texte f^k ;
- représentation XML<power><base>f</base><exponent>g</exponent></power>,
- représentation latex f^{g}.

Tâche 31 : Créez les classes décrites ci-dessus. Vous devez :

Tester les classes que vous créez ;
Faire attention à minimiser la duplication de code ;
Faire attention à respecter les principes SOLID ;
Ajouter les classes dans les fabriques abstraites ;
Ajouter les classes aux différents visiteurs ;
Modifier FormulaParser pour ajouter les opérations correspondant aux nouveaux types de formules.