Exemple: le rendu de monnaie

Entrées:

une liste \([v_1,\ldots,v_n]\) d’entiers en ordre décroissant, un entier \(S\)

Sortie:

une liste \([p_1,\ldots,p_n]\) telle que \(p_1v_1+\cdots+p_nv_n=S\), avec \(p_1+\cdots+p_n\) minimal

p := [0, 0, ..., 0]
pour chaque i de 1 à n:
    tant que v[i] <= S:
        p[i] := p[i] + 1
        S := S - v[i]

Principe général

Les algorithmes dits gloutons servent à résoudre certains problèmes d’optimisation.

• On procède de façon séquentielle, en faisant à chaque étape le choix qui semble localement le meilleur.

• On ne revient jamais en arrière.

• Il s’agit d’une progression descendante, à chaque étape on fait un choix puis on résoud un problème plus petit issu de ce choix.

En général, le fait que le résultat soit correct est facile, le fait qu’il soit optimal n’est pas évident.

Problème du choix d’activités

On a un ensemble d’activités, chacune caractérisée par une heure de début et une heure de fin, qui veulent utiliser une même ressource.

Entrées:

un ensemble fini \(A\),
deux fonctions \(d,f:A\to\mathbb{R}^+\) avec \(d(a) < f(a)\)

Sorties:

un sous-ensemble \(S \subseteq A\) de cardinal maximal tel que pour tous \(a \neq b \in S\), \({[d(a);f(a)[}\cap{[d(b);f(b)[}=\emptyset\)

Exemple

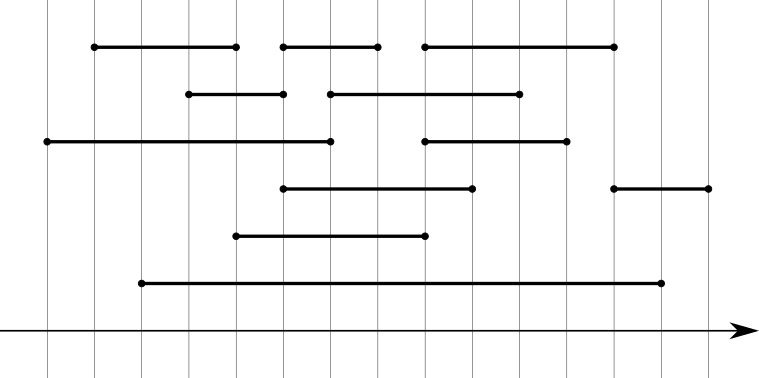
Solution

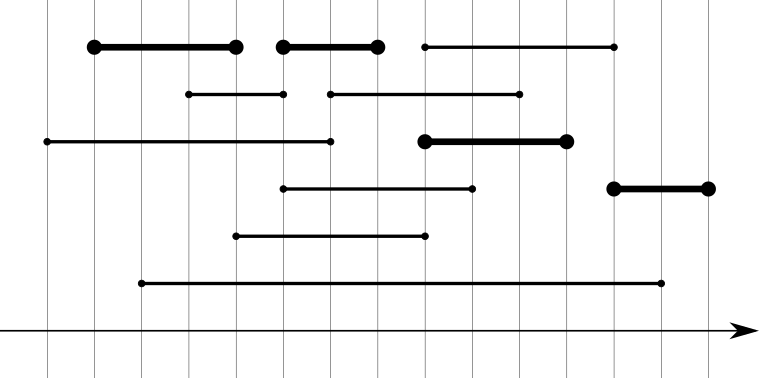
Algorithme glouton

Trame générale:

trier A selon un critère approprié
S := { }
pour chaque a dans A:
    si a est compatible avec tous les éléments de S:
        S := S + { a }
renvoyer S

Quel critère faut-il appliquer?

• par heure de début?
• par heure de fin?
• par nombre de conflits?

Algorithme glouton, par heure de fin

trier A par valeurs croissantes de f
S := { }
t := 0
pour chaque a dans A:
    si d(a) >= t:
        S := S + { a }
        t := f(a)
renvoyer S

Coût en temps de l’algorithme: \(O(n \log n)\)

• le tri initial est en \(O(n \log n)\)
• la boucle est en temps linéaire, \(O(n)\)

Observations

• Deux activités \(a\) et \(b\) sont compatibles si et seulement si \(f(a) \leq d(b)\) ou \(f(b) \leq d(a)\).

• Une solution est un sous-ensemble maximal d’éléments deux-à-deux compatibles.

• Dans une solution \(\{a_1,\ldots,a_m\}\) ordonnée par heure de fin croissante, on a donc \[ d(a_1) < f(a_1) \leq d(a_2) < f(a_2) \leq \cdots \leq d(a_m) < f(a_m) \]

Correction de l’algorithme

Soit \(S=\{a_1,\ldots,a_m\}\) le résultat renvoyé par l’algorithme, avec \(f(a_1) \leq \cdots \leq f(a_m)\). On montre par récurrence que pour tout \(k \leq m\), il existe une solution optimale qui commence par \(a_1,\ldots,a_k\).

• Soit une solution optimale \(T\) qui contient \(a_1,\ldots,a_k\), pour un certain \(k<m\). Soit \(b\) l’élément suivant \(a_k\) dans \(T\). Alors:

  • \(f(a_{k+1}) \leq f(b)\) (par construction de l’algorithme)
  • pour tout \(e \in T\setminus\{a_1,\ldots,a_k,b\}\), on a \(d(e) \geq f(b) \geq f(a_{k+1})\) (parce que les éléments de \(S\) sont compatibles entre eux)

  donc \(T\setminus\{b\}\cup\{a_{k+1}\}\) est une solution.
  Elle a même cardinal que \(S\) et elle contient \(a_1,\ldots,a_{k+1}\).

• Le cas initial \(k=0\) est immédiat.

Par conséquent \(S\) est une solution optimale.

Problème

• Graphe: \(G=(S,A)\), avec \(S\) ensemble des sommets, \(A\) ensemble d’arêtes (non orientées)
• Graphe pondéré: graphe avec une fonction \(w:A\to\mathbb{R}^+\)
• Arbre couvrant: sous-ensemble d’arêtes \(T \subseteq A\) connexe, sans cycle et qui touche tous les sommets
• Poids d’un sous-ensemble \(T \subseteq A\): \(w(T)=\sum_{a\in T} w(a)\)

Exemple

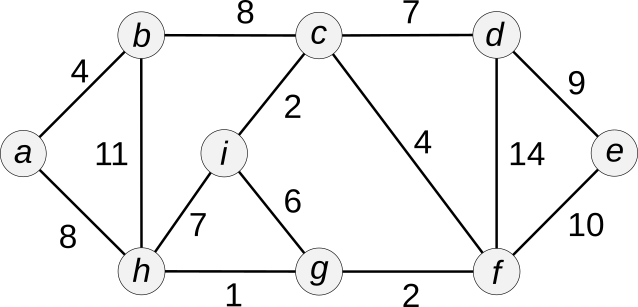
Solution (de poids minimal plutôt que maximal, ici)

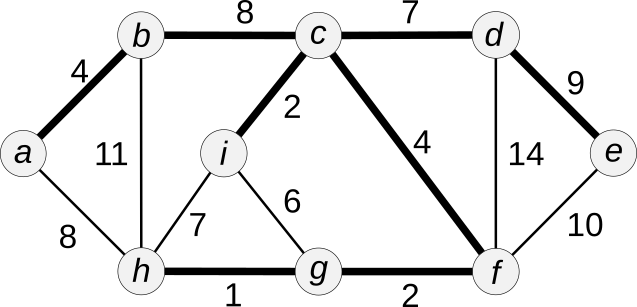
Algorithme de Kruskal

On se donne un graphe connexe \(G=(S,A)\) et une pondération \(w\).

T := { }
pour chaque a dans A, par valeurs décroissantes de w:
    si T + { a } est acyclique:
        T := T + { a }
renvoyer T

Remarques

• L’algorithme renvoie forcément un arbre couvrant:

  • \(T\) est toujours acyclique,
  • il n’est pas possible d’ajouter une arête à \(T\) sans le rendre cyclique (sinon l’algorithme l’aurait fait).

• Tous les arbres couvrants on le même nombre d’arêtes
  (= nombre de sommets – 1).

• Reste à montrer que le poids de l’arbre obtenu est maximal.

Lemme d’échange

Démonstration:

• \(U \setminus \{a\}\) a deux composantes connexes \(U_1\) et \(U_2\).
• \(T \cup \{a\}\) a un cycle qui passe par \(a\), ce cycle a un nombre pair d’arêtes entre \(U_1\) et \(U_2\).
• En prenant \(b\) entre \(U_1\) et \(U_2\) dans ce cycle, on obtient le résultat voulu.

Correction de l’algorithme de Kruskal

Soit \(T\) l’arbre renvoyé par l’algorithme.
Supposons que \(T\) n’est pas de poids maximal.

• Soit \(U\) un arbre couvrant tel que \(w(U)>w(T)\) avec \(T \cap U\) de cardinal maximal.
• Soit \(a \in U \setminus T\) dont le poids est maximal.
  Le lemme d’échange donne un \(b \in T \setminus U\) tel que \(U':=U \setminus \{a\} \cup \{b\}\) est un arbre couvrant.
• Par construction de l’algorithme, on a nécessairement \(w(b) \geq w(a)\) (sinon \(a\) aurait été choisi avant \(b\) dans \(T\)).
• Alors \(w(U') = w(U)-w(a)+w(b) \geq w(U) > w(T)\).
• Or \(U'\) a une arête de plus que \(U\) en commun avec \(T\), contradiction.

Donc \(T\) est de poids maximal.