Schéma global

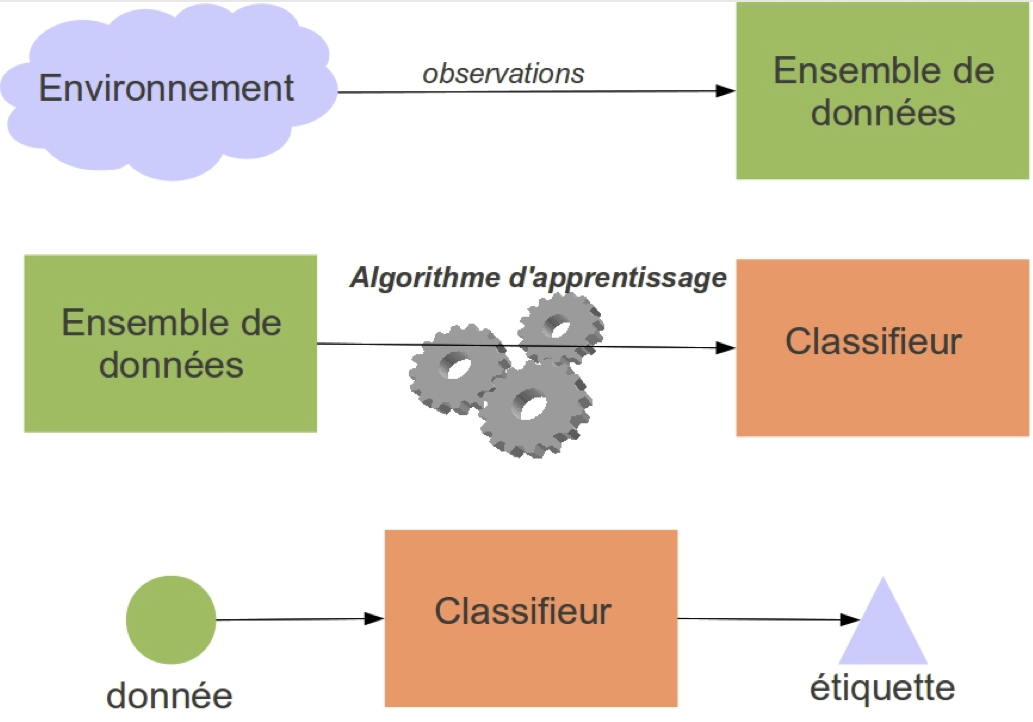
Science des données

• Analyse de données : aller plus loin que les statistiques descriptives
• But : extraire automatiquement des données la connaissance permettant de prendre des bonnes décisions à l’avenir (sur d’autres / de nouvelles données)
• Moyen : inférer un modèle (mathématique…) qui capture les régularités observables dans les données d’apprentissage (principe de généralisation)

Exemple

Alors que vous venez juste d’atterrir au Groland pour la première fois, vous apercevez un mouton noir. Quelles conclusions en tirer ?

• Il y a un et un seul mouton noir au Groland : apprentissage par coeur, sous-généralisation
• Certains moutons sont noirs au Groland
• Tous les moutons du Groland sont noirs : sur-généralisation

Sous-, sur-, correcte généralisation

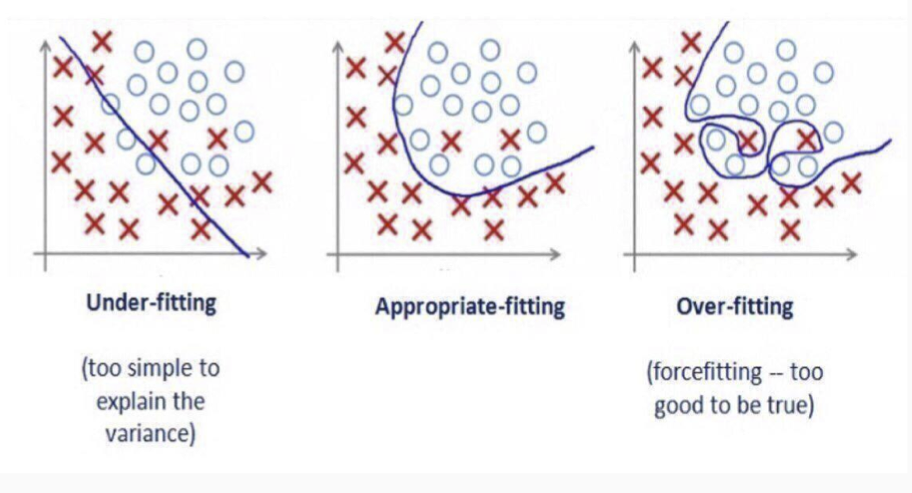
Classification supervisée : de vraies applications

• But : écarter automatiquement les SPAM et autres messages non sollicités.
• Données : des messages dont on sait s’ils sont des SPAMs ou non.
• Objectif : construire un classifieur, capable d’attribuer une de ces deux classes à un nouveau message.

Données

• Attributs : un ensemble \(X = X_1 \times X_2 \times \cdots \times X_d\) où chaque \(X_i\) est le domaine d’un attribut \(A_i\) numérique.

Exemple : \(A_1=\)age, \(X_1= [0;122]\), \(A_2=\)fumeur, \(X_2=\{0,1\}\) (non/oui)

• Classes (ou étiquettes) : un ensemble fini de classes \(Y\).

Exemple : \(Y = \{\)patient à risque, patient sans risque\(\}\)

Données

Classifieur

\[ f\colon X\to Y \]

Exemple : \(f(x) =\) Si fumeur=‘oui’ et age > 59 alors ‘risque’ sinon ‘pas risque’

• Fonction de perte (loss function) : \(L(y_i, f(x_i)) = 0\) si \(y_i = f(x_i)\) et 1 sinon.

Exemple : \(L('risque', f((35, 'oui'))) = 1\) et \(L('risque', f((65, 'oui')) = 0\)

Principe

• Objectif : pouvoir prédire la classe d’un nouvel exemple en utilisant les exemples déjà connus

• Principe :

  1. Regarder la classe des \(k\) exemples les plus proches
  2. Affecter la classe majoritaire dans le voisinage du nouvel exemple

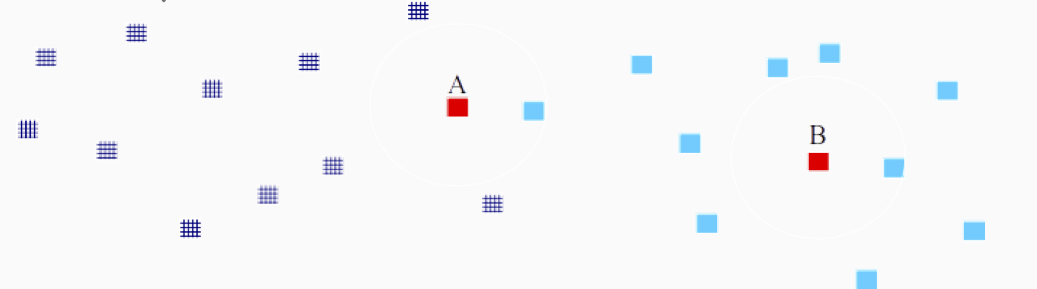
Algorithme des \(k\) plus proches voisins

• Entrée : \(S =\{(x, y) \mid x \in X \subseteq \mathbf R^d, y \in Y \subseteq \mathbf R\}\) l’échantillon d’apprentissage de taille \(n\), \(x_{test}\) l’exemple à classer

Initialiser à 0 le nombre d'occurrences de chaque classe
Pour chaque exemple (x, y) dans S :
    Calculer la distance D(x, xtest)
k-voisinage := k plus proches voisins de xtest
Pour chaque x' dans k-voisinage, associé à la classe y' :
    Ajouter 1 au nombre d'occurrences de la classe y'
Retourner la classe la plus fréquente

Comment calculer les \(k\) plus proches voisins ?

• Extraction des \(k\) minimums un par un : \(\mathcal O(kn)\)

Que faire en cas d’égalité ?

Et si 2 classes ou plus sont aussi fréquentes dans le k-voisinage ?

On peut :

• Augmenter \(k\) de 1
• Tirer une classe au hasard parmi les plus fréquentes
• Attribuer la classe majoritaire dans les données
• Pondérer les exemples par leur distance à la donnée à classer

Limites

• Nécessite une notion de distance pertinente pour la classification
• Complexité en \(\mathcal O((k+d)n)\) ne passant pas à l’échelle :
  • réduction de l’échantillon d’apprentissage a priori,
  • réduction de la taille des données (analyse en composantes principales),
  • organiser les données dans des structures permettant d’accélérer la décision…

Validation d’un apprentissage

Plusieurs méthodes permettent de valider (ou d’infirmer) la qualité d’un processus d’apprentissage.

Une des approches consiste à n’utiliser qu’une partie des données pour apprendre et à se servir des autres données pour tester le résultat.

Différentes mesures permettent alors de comparer des processus (taux d’erreur, F-score, etc.)

D’autres méthodes d’apprentissage ?

• Arbres de décision
• Perceptron
• Réseaux de neurones

Bloc 4 du DIU EIL !