The goal
Quantitative games are two-player zero-sum games played on directed weighted graphs. Total-payoff games—that can be seen as a refinement of the well-studied mean-payoff games—are the variant where the payoff of a play is computed as the sum of the weights. This tool proposes a pseudo-polynomial time algorithm for total-payoff games in the presence of arbitrary weights. It consists of a non-trivial application of the value iteration paradigm. Indeed, it requires to study, as a milestone, a refinement of these games, called min-cost reachability games, where we add a reachability objective to one of the players. For these games, the tool also provides an efficient value iteration algorithm to compute the values and optimal strategies (when they exist), that runs in pseudo-polynomial time. We also propose heuristics allowing one to possibly speed up the computations in both cases.
The tool is an add-on to PRISM-games, an extension with stochastic games of the open-source statistical model-checker PRISM.
Download and installation
- The article with the theoretical background, and formal proofs of correctness
- Source code and binary files (compiled for Mac OS X Yosemite with Java 8). The executable file prism is in the /bin directory: to set the path correctly, make sure to first run
./install.sh
Notice that our tool is an add-on to the development version of PRISM-games, and hence contains the PRISM tool publicly available at that release. Please check first if it is executable on your system. If it is not the case, the main directory contains a Makefile that should work on all platforms. Simply typesudo make
in a terminal to launch the compilation. It produces the executable files in the /bin directory. Make sure to add this path to the PATH variable to use freely the executablesexport PATH=$PATH:/path/to/TP-MCR-tool/bin/
- Some examples of the new capabilities. See the pdf file to see pictures and expected results for the examples in the repository. The archive contains two executable scripts to run some useful tests on these examples.
Usage
We only describe here the differences and novelties in usage with respect to PRISM-games. Check here for an introduction to the PRISM-games syntax and running methods.
Our models with total-payoff and min-cost reachability objectives are indicated by the keyword game. Our primary goal is the study of non-stochastic games (only non-deterministic choices). The set of all players and the distributions under their control is specified using one or more player... endplayer constructs, as in the example below.
game player Min arena endplayer player Max [a], [b] endplayer const int W; const int n; module arena s : [1..2*n+1] init 2; [] mod(s,2)=0 -> (s'=s+1); [] mod(s,2)=0 -> (s'=s-1); [a] s<=2*n & mod(s,2)=1 -> (s'=s+1); [b] s<=2*n & mod(s,2)=1 -> (s'=s+2); [] s=2*n+1 -> (s'=2*n+1); endmodule label "T" = s=2*n+1; rewards [a] true : -1; [b] true : -w; endrewards
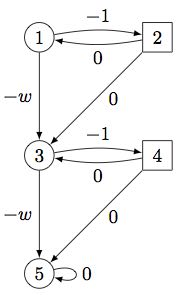
For example, the above model has two players Min and Max. The number of states is parametric, i.e., 2n+1 with a constant n to be defined later. Max controls actions labelled a and b, and Min controls all the other actions. As in PRISM, we can model games by using several components synchronising through shared labels. However, as for PRISM-games, our tool only supports turn-based games, in which all the choices available in a given state are controlled by the same player. Label T is used to denote the target set of states, here a single state. The reward structure is defined with the player... endplayer construct: here again, one of the reward is parametrized by a constant w to be defined later. In case n=2, the game arena is depicted below.
Even though, we have kept the capability to model-check the full logic rPATL (no exact reward check however), as in PRISM-games (however, without probability distributions), the main novelty lies in the new verification method for reward properties related with total-payoff and min-cost reachability objective, such that:
// The minimum value of reward accumulated before // reaching "T" that can be guaranteed by player Min <<Min>> Rmin=? [F "T"] // The maximum value of reward accumulated before // reaching "T" that can be guaranteed by player Max <<Max>> Rmax=? [F "T"] // The minimum value of total-payoff // that can be guaranteed by player Min <<Min>> Rmin=? [Fc false] // The maximum value of total-payoff // that can be guaranteed by player Max <<Max>> Rmax=? [Fc false]
Because of some determinacy results, in all our games, the two first values, as well as the two last ones, are known to be always identical. For the previous example, we will obtain -2w for the four properties. It is also possible to ask whether a given threshold on the reward can be guaranteed for a player, and hence, nest the different queries:
// Player Max has a strategy to ensure that // the total-payoff is at least -w <<Max>> R>=-w [Fc false] // The minimum value of reward accumulated before // reaching the set of states verifying the previous property // that can be guaranteed by player Min <<Min>> Rmin=? [F (<<Max>> R>=-w [Fc false])]
For the previous example, only states 3, 4 and 5 verify the first property, so that the last query outputs value -w.
Notice finally that our tool can handle some probabilistic choices in the arena, though we do not currently guarantee the output results for all stochastic games.
Contact
PRISM is an open-source statistical model-checker, created and actively maintained by:
- Dave Parker (University of Birmingham)
- Gethin Norman (University of Glasgow)
- Marta Kwiatkowska (University of Oxford)
This extended version is based on the development version (r9679) of PRISM-games, and has been implemented by Benjamin Monmege
- E-mail: benjamin.monmege at ulb.ac.be
-
Address ULB - Campus de la Plaine
Office N8 207
CP212 - 1050 Bruxelles - Belgium
- Phone +32 2 650 58 57