Homologie algorithmique

Contexte

Topologie études des espaces (objets) à déformation près → invariants topologiques

Homologie théorie calculable qui permet de définir et de compter les trous

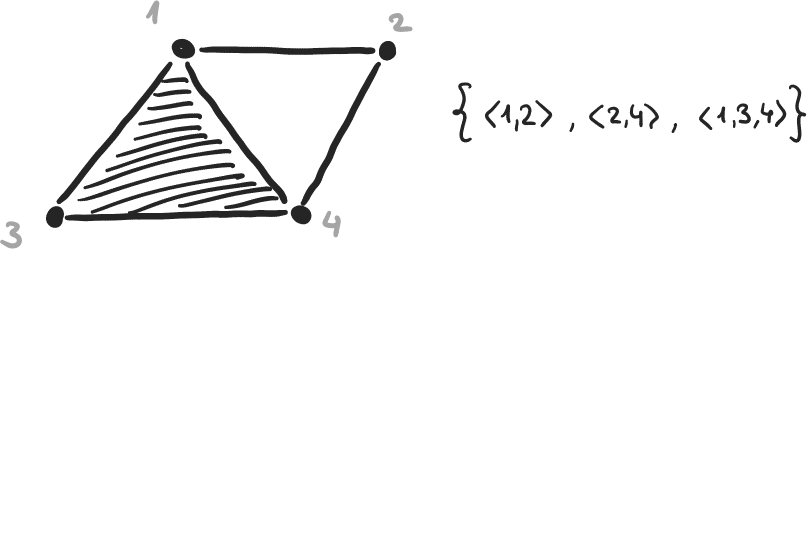
Complexe simplicial, incidence :

Cycles, classes d'équivalence, base d'homologie :

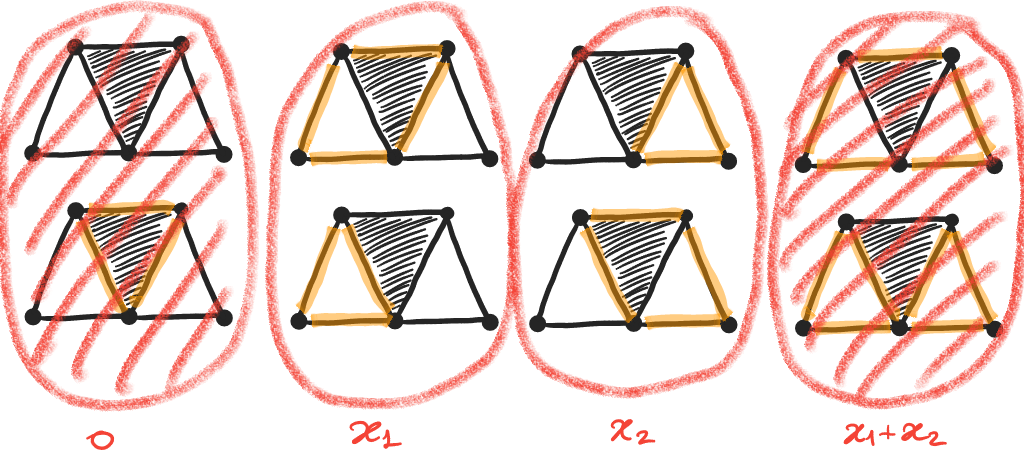
Formellement :

\(K\) : complexe simplicial fini
\(K_q\) : simplexes de \(K\) de dimension \(q\)
\( (C, \partial) \) : complexe de chaînes induit par \(K\) avec anneau de coefficients = \(\mathbb{Z}/2\mathbb{Z} \) (corps)
\(H_q = \ker(\partial_q) / \text{im}(\partial_{q+1}) \) : groupe d'homologie de dimension \(q\) de \(K\) (espace vectoriel)
\(\beta_q = \dim(H_q)\) = nombre de Betti de dimension \(q\)

Nombre de trous : composantes connexes, tunnels, cavités...

Les groupes d'homologie sont calculables :

Complexe simplicial \( K \) ≃ liste de tuples
liste de tuples ≃ matrices de bord,
\( \partial_{q+1}(\langle v_1, \cdots, v_q \rangle) = \sum_{i=1}^q (-1)^{i+1} \cdot \langle v_1, \cdots, \hat{v}_i, \cdots, v_q \rangle \)
\( H_q(K) = \ker(\partial_q) / \text{im}(\partial_{q+1}) = (\mathbb{Z}/2 \mathbb{Z})^{\beta_q} \)
\( \beta_q = \dim(\ker(\partial_q)) - \dim(\text{im}(\partial_{q+1})) \)
\( \dim(\ker(\partial_q)) \), \( \dim(\text{im}(\partial_{q+1})) \) ? ⟶ Diagonalisation

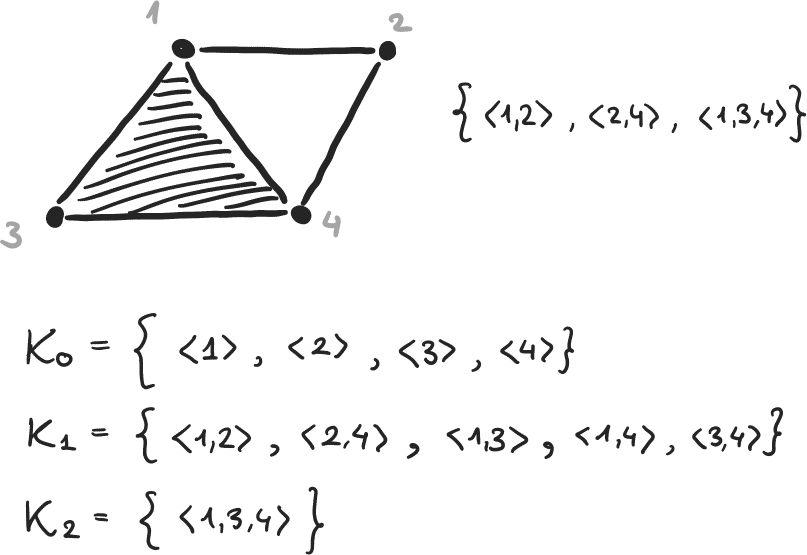
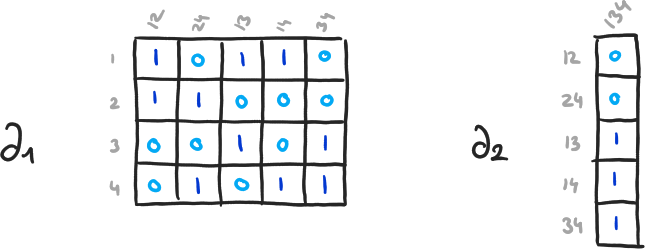
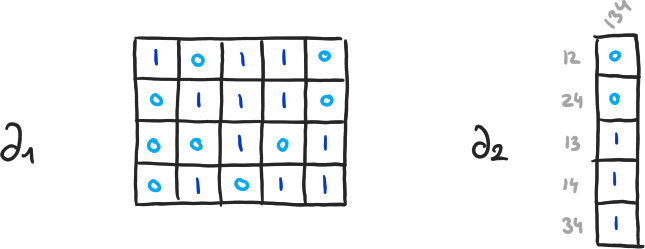
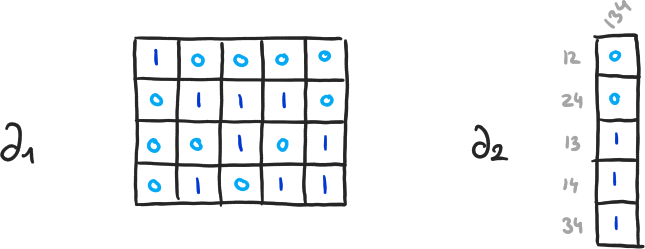
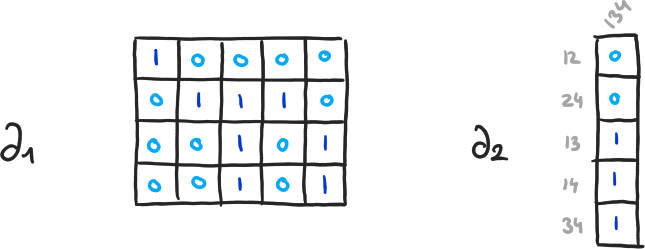
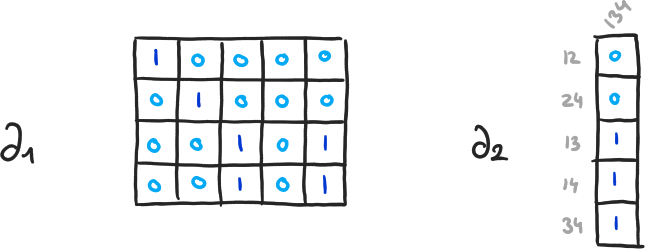
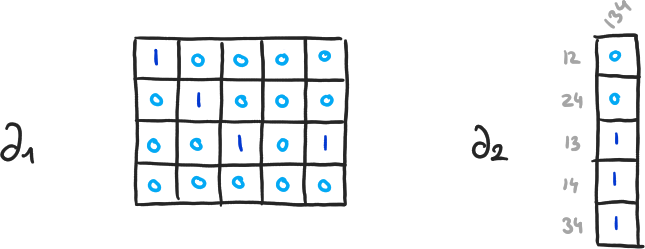
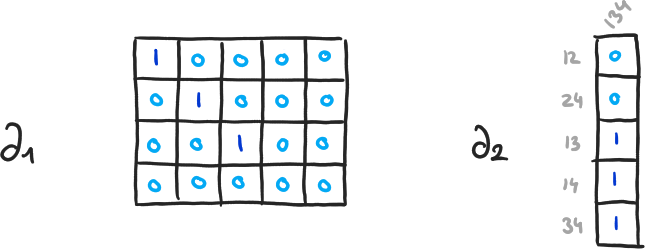
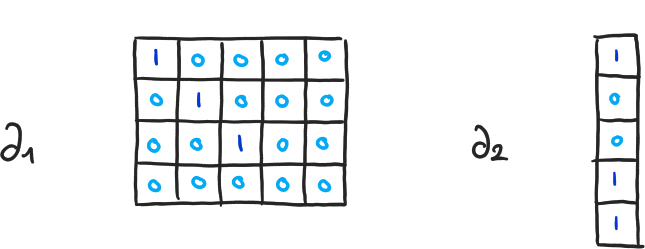
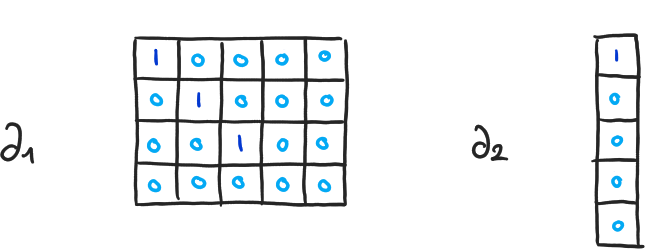
\( \beta_0 = 4-3, \beta_1 = 2-1, \beta_2 = 0-0 \)

Filtration : suite de complexes imbriqués \[K^1 \subset K^2 \subset \cdots \subset K^n\]

On peut définir les paires de persistance : instants de naissance et mort de chaque trou
Trou qui dure longtemps ≃ feature important
Très bonne propriété de stabilité si les données sont bruitées

Les trous dans un maillage sont bien définis et on peut les calculer en \( \mathcal{O}(n^3)\)

Structure combinatoire pour manipuler les groupes d'homologie (pas seulement le nombre de trous)

Une application : recalculer l'homologie après une modification

Question : comment distinguer les trous d'un objet ?

Érosions + dilatations = filtration

\( D_q \cap Q^{0,0} \) = \( \beta_q \) paires \( (- a_i, b_i) \) avec \( a_i, b_i \geq 0 \)
Une paire \( (a_i, b_i) \) pour chaque trou
\( a_i \) : de combien il faut éroder l'objet pour casser ce trou
= épaisseur
\( b_i \) : de combien il faut dilater l'objet pour remplir ce trou
= largeur

De plus, le couplage de l'algorithme de l'homologie persistante permet de définir les deux centres de chaque trou

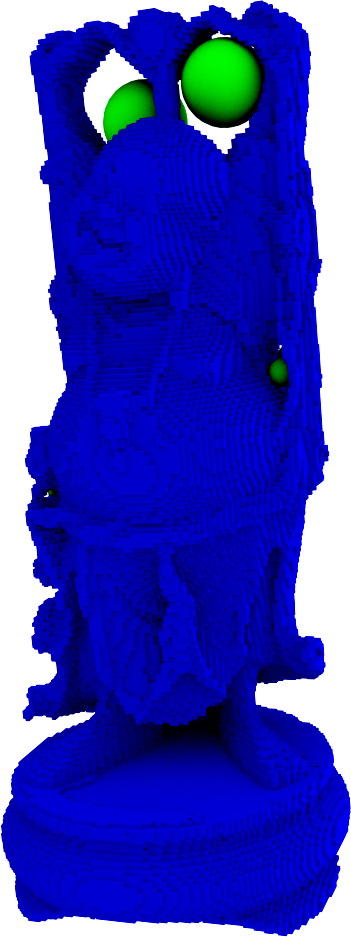
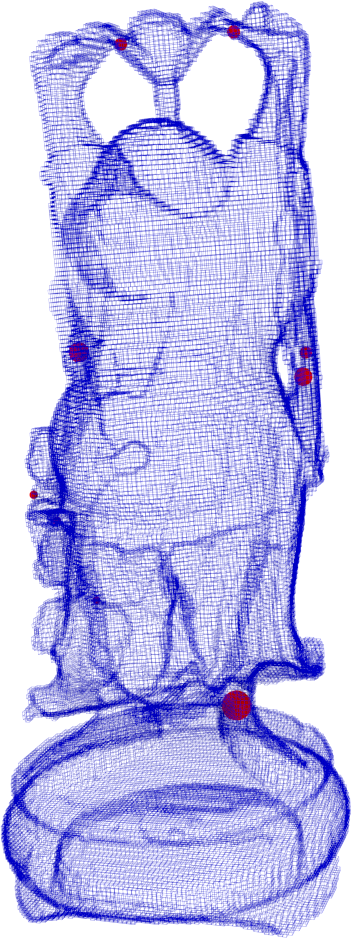
Une application : générateurs d'homologie courts